(Capítulo 23.4 – Exercício 10) A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de de aresta, imersa em um campo elétrico dado por, com em metros. Qual é a carga total contida no cubo?
Passo 1
Faaala galera, tudo certinho?
Nesse exercício, temos um cubo de lado .
N, nesse cubo passa o campo, , e aí precisamos descobrir a carga total contida no cubo.
Podemos utilizar a lei de Gauss para descobrir a carga contida no cubo, porém para isso, precisamos calcular o fluxo elétrico que atravessa o cubo.
, pPara calcular o fluxo elétrico, isso podemos utilizar a formulafórmula:
Onde:
é o fluxo elétrico que atravessa o cubo;
é o campo elétrico e
é a derivada da área atravessada.
Antes de fazer essa integral, vamos pensar o seguinte: quando eu tenho um campo elétrico constante atravessando a superfície, esse campo não tem importância para o fluxo total que atravessa a superfície, pois tudo que entra, devido a esse campo, sai
LOGO, só estamos interessados em quem irá variar!
Se olharmos para o campo que é dado no enunciado, podemos descartar de cara as componentes y (), z () e a componente constante do x (), pois elas NÃO VARIAM com a posição!
Podemos fazer toda a conta com essas componentes? Podemos, mas no final só estaríamos fazendo contas a mais que vão zerar.
Então vamos aplicar isso
Passo 2
Como a nossa única componente que varia com a posição é a componente do eixo do campo elétrico, dada por , vamos calcular o fluxo, somente levando em conta a face frontal e traseira, porque são elas que variam o :
Onde:
Aqui temos o campo onde ,a face que está na origem do eixo .
Enquanto:
A face traseira do cubo está na parte negativa de e se o cubo tem lados iguais a , essa face traseira está em .
Aqui temos os nossos fluxos, e eles são dados por produtos escalares. Para saber se esses produtos escalares vão dar positivo ou negativo, uma boa forma de se ver é pensar que:
Fluxo que está saindo da superfície é positivo.
Fluxo que está entrando na superfície é negativo.
Olhando para a nossa figura, temos:
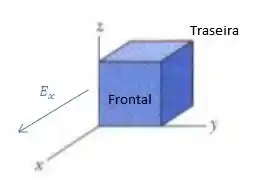
Vemos então que o fluxo ocasionado pela componente do campo elétrico na face traseira está entrando na superfície e, portanto, o nosso produto escalar dá negativo:
E o fluxo na frontal está saindo, portanto o produto escalar dá positivo:
Passo 3
Se o campo é dado só pela componente que varia o , então será:
Vamos substituir então na equação?
Substituindo os fluxos:
Substituindo os campos e seus pontos :
Multiplicando, temos:
E qual é a área de um quadrado com aresta igual a Sim, a área é igual a
Então, o fluxo finalmente é:
Passo 4
Agora, utilizando a lei de Gauss para encontrar a carga, essa lei diz que o fluxo elétrico
É igual a divisão do valor da carga interna pela permissividade elétrica do meio, logo:
Substituindo o valor do campo elétrico que calculamos e o valor da permissividade elétrica :
Ufa, essa foi longa hahahaha