Halliday - Vol. 3 – 9º edição – Capítulo 23 – Seção 8 – Exercício 40
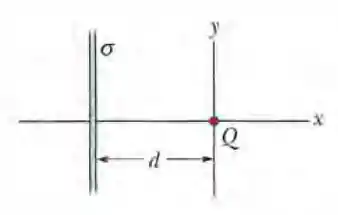
(Capítulo 23.8 – Exercício 40) A Fig. 23-46 mostra uma placa não condutora muito extensa que possui uma densidade superficial de cargas uniforme ; a figura mostra também uma partícula de carga , a uma distância da placa. Ambas estão fixas no lugar. Se , para que coordenada (a) positiva e (b) negativa sobre o eixo (além do infinito) o campo elétrico total , é zero? (c) Se , para que coordenada sobre o eixo x o campo
é zero?
Passo 1
Eaeee gente, nesse exercício vamos usar os conceitos da simetria planar na Lei de Gauss
Primeiro, pare e pense: em qual posição do eixo acima uma partícula carregada poderia estar em equilíbrio, quando ?
Veja que o único lugar onde isso não é possível é a região entre a placa e a carga, por que os campos elétricos gerados por elas nessa região estão no mesmo sentido.
Então vamos manter esse raciocínio usando a teoria da coisa
Passo 2
a) Então vamos supor um ponto localizado à direita da placa, de uma distância . A condição necessária para que o campo nessa região se anule é a seguinte:
Isolando :
Substituindo os valores:
Então a coordenada positiva é:
Passo 3
b) A coordenada negativa, nesse caso, é igual a , devido à simetria e ao resultado do item a 😉
c) Veja que, se m, um dos pontos (o de abscissa ) já fica fora da região de equilíbrio permitida. Daí, nesse caso, o único ponto de equilíbrio é aquele em que , show?