Halliday - Vol. 3 – 9º edição – Capítulo 23 – Seção 9 – Exercício 45
(Capítulo 23.9 – Exercício 45) Duas cascas esféricas concêntricas carregadas têm raios de 10,0 e. A carga da casca menor é e a da casca maior é . Determine o campo elétrico (a) em ; (b) em .
Passo 1
Faaala galera, vamos lá continuar falando sobre a Lei de Gauss?
Esse exercício a gente vai resolver analisando sempre o que a gaussiana envolve, beleza? Após isso usaremos a equação do campo elétrico com as cargas envolvidas na gaussiana.
Então boraaa
Passo 2
O item a. pede pra gente calcular o campo elétrico numa distância de , vamos ver o que acontece? Se liga no desenho.
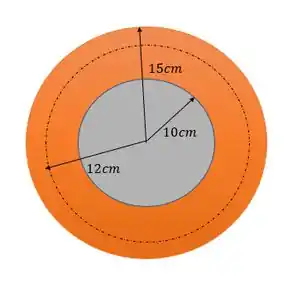
Em , somente contabilizamos a carga da casca de de raio por que apenas ela é abrangida pela superfície gaussiana esférica de raio .
Como contabilizremos apenas o campo elétrico vai ficar:
Substituindo-se os valores e :
Passo 3
No item b. o raio considerado é , nessa região todas as cargas estão envolvidas na gaussiana, se liga aí:
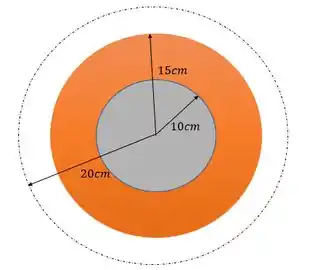
Nesse caso o campo será dado por:
Aqui substituindo a carga e carga e o raio temos:
E é isso aí!!