UFSC – Cálculo 1 – Lista 4.2 – Questão 8
Use o item (i) do exercício 7 para resolver a equação diferencial com a condição inicial .
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pede para resolvermos essa equação diferencial
Bom, uma equação diferencial é uma equação que tem como variável a derivada de uma função!
Então quando o problema diz para resolvermos essa equação aqui
Ele está perguntando na realidade qual função que quando for derivada dá a função !
E qual é o nome mesmo que damos a essa função ? De primitiva! Ou seja, queremos saber qual é a integral de ! Ou na forma de integral
Tudo bem até aqui?
E onde entra o item (i)? Entra que nesse item a gente vai calcular justamente a integral de !
Vou resgatar de lá o resultado:
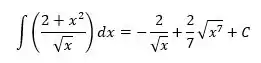
Sabe esse ? É agora que vamos usar a condição inicial! Vamos descobrir qual é a solução específica que satisfaz esse ponto!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Já descobrimos que queremos a solução e que ela é a integral daquela função lá do passo anterior:
E usando o resultado já calculado (se você tem dúvidas, dá uma espiadinha na lista 4.2, questão 7 item (i), beleza?) temos o seguinte:
Tranquilo?
Passo 3
Agora vamos aplicar a condição inicial :
Então encontramos qual constante que satisfaz a condição inicial
E assim encontramos a solução da equação diferencial:
Beleza? E é isso!
Espero ter ajudado! Vamos para a próxima?