Considere com produto interno canônico. Seja uma transformação linear dada por:
T é autoadjunta? T é ortogonal? Justificar.
Defina operador adjunto e operador ortogonal.
Passo 1
Vamos começar definindo o que é um operador autoadjunto e um operador ortogonal.
Um operador T é autoadjunto se e só se a matriz que representa T for simétrica, ou seja, se A é a matriz que representa T, então T é adjunto se e somente se:
Já um operador T é ortogonal se e só se a matriz A que representa T satisfizer:
Onde I é a matriz identidade.
Passo 2
Agora sabemos que para verificar se T é autoadjunta, precisamos ver se a matriz que a representa é simétrica.
Vamos considerar a base canônica do . A matriz da transformação linear T vai ser dada por:
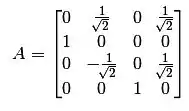
Fazendo a transposta:
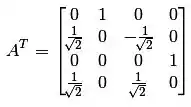
Como:
A não é simétrica, logo T não é adjunta.
Passo 3
Vamos verificar se A é ortogonal. Fazendo o produto:

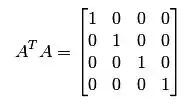
Como:
Então T é ortogonal.
Resposta
T não é adjunta.
T é ortogonal.
T é autoadjunta se e somente se a matriz A é simétrica.
T é ortogonal se e somente se a matriz A é ortogonal.