Seja um espaço vetorial munido com produto interno usual. Considere os vetores de e um operador linear tal que e
(a) Verifique se T é auto-adjunto.
(b) Verifique se T é ortogonal.
Passo 1
Vamos começar definindo o que é um operador auto-adjunto e um operador ortogonal.
Um operador T é autoadjunto se e só se a matriz que representa T for simétrica.
Ou seja, se A é a matriz que representa T, então T é adjunto se e somente se:
Já um operador T é ortogonal se e só se a matriz A que representa T satisfizer:
Onde I é a matriz identidade.
Vamos verificar isso para o operador dado, mas antes precisamos achar a matriz que representa essa transformação T.
Passo 2
Temos que:
É uma base ortonormal de V.
Vamos escrever a matriz , a matriz que representa T na base
Pra isso, aplicamos a transformação aos vetores da base e escrevemos os resultados em termos de coordenadas da base nas colunas de uma matriz.
Fazendo isso:
Então:
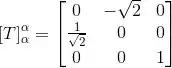
Passo 3
(a) A transposta dessa matriz é:
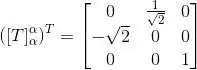
Como:
O operador não é auto-adjunto.
Passo 4
(b) Vamos fazer o produto para verificar se T é ortogonal.
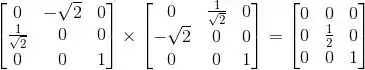
Como essa matriz não é a identidade, T não é ortogonal.
Resposta
(a) Não é auto-adjunto
(b) Não é ortogonal