Seja a transformação linear dada por

(a) Mostre que a matriz de na base canônica de é:

(b) Determine os autovalores de .

(Dica na conta: .)

(c) Determine os autoespaços de .

(d) é sobrejetora?

(e) Existe uma base ortonormal de feita de autovetores de ? Se sua resposta foi afirmativa, exiba uma base ortonormal de feita de autovetores de . Se sua resposta foi negativa, justifique.

(f) é ortogonalmente diagonalizável? Se sua resposta foi afirmativa, diagonalize ortogonalmente. Se sua resposta foi negativa, justifique.

(g) Use a definição de e dê uma justificativa geométrica para encontrar novamente os autoespaços de .

(h) Use a definição de e dê uma justificativa geométrica para encontrar novamente os autovalores de .

b)

Vamos achar o polinômio característico:

Usando a dica do enunciado:

Logo, os autovalores são: e

c)

Para achar os autoespaços é só aplicar os autovalores na matriz e resolver os sistemas:

Vamos resolver escalonando:

Voltando para as equações:

Substituindo na primeira:

Logo,

Agora o próximo autovalor:

Vou passar para a forma de equações para reorganizer o sistema:

Tenho então que

d) Para ser sobrejetora, a imagem deve ser igual ao contradomínio, o Para isso, deve ter dimensão igual a 3.

Sabemos que o autoespaço associado ao autovalor é o núcleo e na letra c) descobrimos que ele tem apenas 1 vetor na base, ou seja, dimensão 1.

Como temos a dimensão do núcleo e queremos a da imagem, o caminho mais fácil para sair desse problema é usando o TNI:

Logo, e por isso, a transformação não é sobrejetiva.

e) Sim, pois a matriz é simétrica!

Vamos achar essa base ortonormal então.

Repara que o espaço é o plano e o vetor ortogonal a ele, vai ser Isso porque suas coordenadas são os coeficientes das variáveis!

Opa, mas gera meu , logo os espaços são perpendiculares entre si, posso dizer que

Para achar minha base ortonormal vou pegar então, primeiramente, um vetor do plano e o vetor ortogonal:

Agora, queremos um outro vetor, pertencente à que seja perpendicular a

Temos um sisteminha linear:

Substituindo na primeira equação:

Posso pegar qualquer vetor dessa reta, mas vou escolher!

Tenho agora uma base ortogonal:

Só falta normalizar:

Assim, a base ortonormal vai ser:

f) Sim pois pelo teorema espectral, as matrizes simétricas são diagonalizáveis.

Vamos achar , mas se escolhermos como sendo a matriz cujas colunas são a base encontrada no item anterior, teremos uma matriz ortogonal!

Quando a matriz é ortogonal Assim, .

g) Bom, vamos voltar à definição de :

Se tiver a mesma direção de , o produto vetorial será igual a zero e consequentemente:

Logo, os vetores na direção ou seja, os da reta estão contidos no autoespaço associado ao autovalor zero.

Agora, se for ortogonal à ele vai pertencer ao plano cujos coeficientes das variáveis são as coordenadas

Como no só tem 3 direções perpendiculares, o vetor , também vai pertencer a esse plano

Repara aqui comigo, peguei um vetor do e fiz o produto vetorial dele com um vetor perpendicular a ele achando esse vetor vermelhinho perpendicular aos dois.

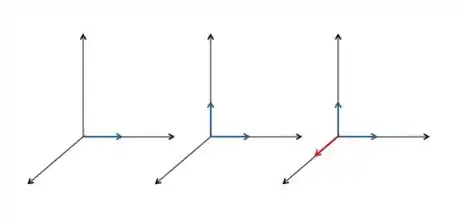
Agora o segundo passo da minha transformação é pegar esse vermelhinho e fazer o produto vetorial dele com o mesmo vetor que fizemos primeiramente:

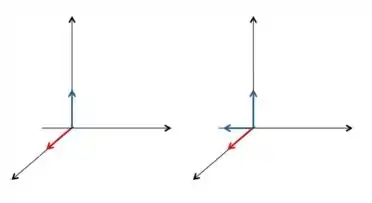
Olha o vetor que achamos após esse produto vetorial, é na mesma direção do que tinhamos inicialmente, nosso Aqui provamos que os vetores que pertencem ao plano mantém a direção apos a transformação, ou seja, são autovetores!

h) Na letra g) já explicamos sobre o autovalor zero.

A norma do vetor é igual a área do paralelogramo formado por esses dois vetores. Como já vimos que eles devem ser perpendiculares, será um retângulo e a área vai ser :

Da mesma forma, a norma de , vai ser:

Assim o módulo do nosso outro autovalor vai ser 3. Entretanto, como vimos no item anterior, o autovetor vai ter sentido oposto do inicial, por causa da regra da mão direita! Assim, o nosso autovalor deve ser