USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.10d
Considere a curva plana dada por
O ponto mais alto da curva é…
Passo 1
Eaew, tudo certinho?
Essa questão é bastante direta, nos foi dada a seguinte curva
e, precisamos nesta alternativa determinar
O ponto mais alto da curva é…
Vamos usar alguns resultados da alternativa anterior! Temos o plot dado por
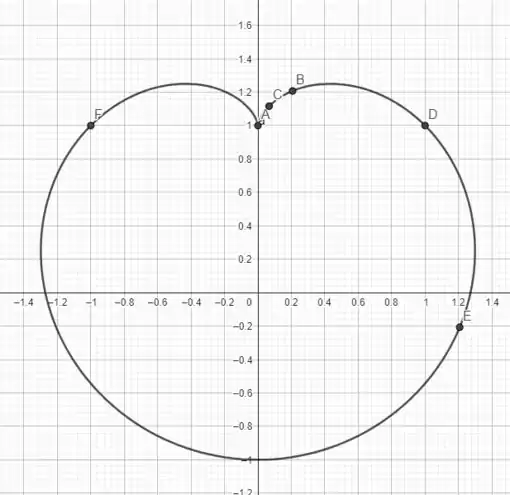
temos dois pontos de mesma altura que serão nossos pontos máximos. Mas, diferentemente do que fizemos nas alternativas anteriores, este ponto máximo é aquele na qual a componente vertical, , da derivada da curva se anula, a derivada foi calculada nos passos anteriores como
Note que existem três pontos em que isso acontece, observe que o gráfico tem dois máximos e um mínimo, vamos ter que usar de outros argumentos para diferenciar entre eles! Vamos lá!
Passo 2
A componente vertical da derivada se anula quando
ou simplificando, quando temos que
no intervalo de à isso acontece em dois valores dentro de nosso intervalo, e , e o valor é equivalente à
Essa questão foi isso! O outro ponto em que a variável é zero está relacionada ao valor mínimo, mas isso é para a próxima alternativa! Te vejo na próxima! Tchau Tchau!