USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.10c
Considere a curva plana dada por
O ponto mais à esquerda da curva é…
Passo 1
Eaew, tudo certinho?
Essa questão é bastante direta, nos foi dada a seguinte curva
e, precisamos nesta alternativa determinar
O ponto mais à esquerda da curva é…
Vamos usar alguns resultados da alternativa anterior! Temos o plot dado por
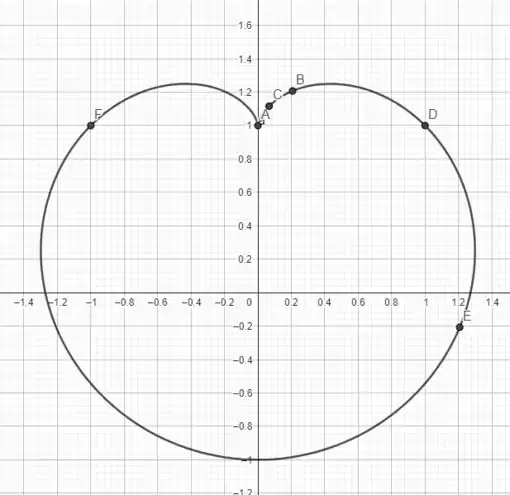
o ponto mais à esquerda será algo entre o ponto e que são para e . O ponto mais à direita será dado por que zera a componente horizontal da derivada da função, na alternativa anterior nós calculamos a derivada da curva como
então precisamos calcular o valor da curva quando
na alternativa anterior também obtivemos
ou
Consegue visualizar qual delas nos dá a reta vertical no lado esquerdo? Vem comigo!
Passo 2
Como na alternativa anterior, temos que a solução não nos ajuda, já que a sua solução não está no intervalo que desejamos. A outra solução, no entanto, nos leva para o maior valor de que encontramos na outra alternativa, essa solução era
Mas, note que a simetria do problema nos ajuda a encontrar o menor valor de já que o cardióide é simétrico em relação ao eixo , então note que podemos identificar os ângulos como
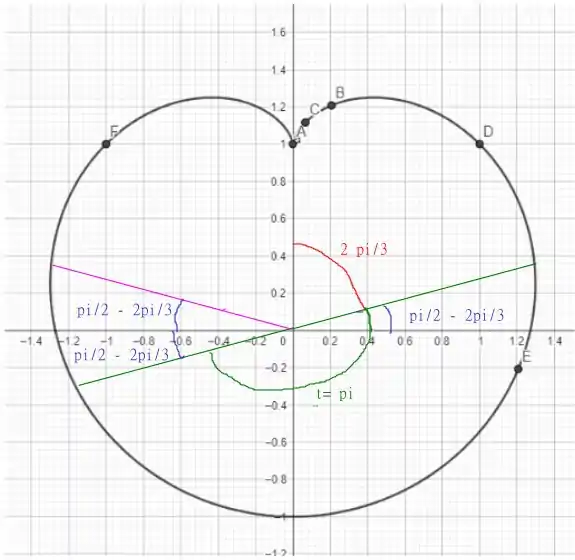
Note que é possível identificar o ângulo de
fazendo a fração final, temos que
Usando este ângulo, temos o ponto da curva como
Essa alternativa foi isso! Vamos para a próxima agora! Até já!