USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.10e
Considere a curva plana dada por
O ponto mais baixo da curva é…
Passo 1
Eaew, tudo certinho?
Essa questão é bastante direta, nos foi dada a seguinte curva
e, precisamos nesta alternativa determinar
O ponto mais baixo da curva é…
Vamos usar alguns resultados da alternativa anterior! Temos o plot dado por
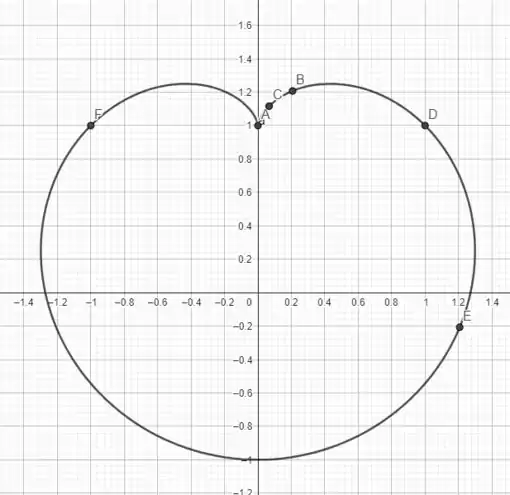
temos apenas um ponto em que a altura é mínima. Assim como fizemos na alternativa anterior, isso ocorre quando a componente vertical, , da derivada da curva se anula, a derivada foi calculada nos passos anteriores como
Note que existem três pontos em que isso acontece, observe que o gráfico tem dois máximos e um mínimo, vamos ter que usar de outros argumentos para diferenciar entre eles! Vamos lá!
Passo 2
A componente vertical da derivada se anula quando
quanto temos que
obtemos os máximos, como foi feito na alternativa anterior, o mínimo ocorre quando temos que
relação verdadeira para , como a derivada não é bem definida em (o gráfico tem uma quina), temos que o próximo valor em nosso intervalo é , em que a curva vale
A questão foi isso! Te vejo na próxima! Tchau Tchau!