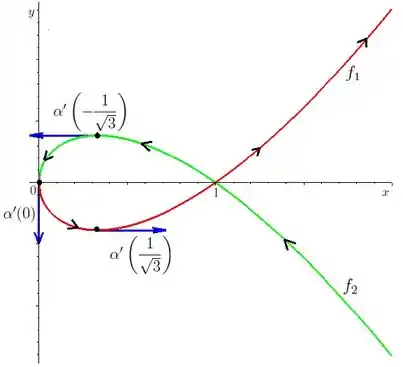
Considere a curva plana parametrizada
- Determine todos os pontos da curva plana nos quais a reta tangente é horizontal ou vertical.
- Determine se o traço da curva plana é simétrico com respeito ao eixo ou ao eixo
- Encontre funções e tais que a união de seus gráficos seja o traço da curva plana dada.
- Com o auxilio das informações obtidas nos itens , e , esboce o traço da curva plana, justificando corretamente o desenho da curva obtido. Identifique em seu desenho a orientação da curva, esboçando o vetor velocidade em três pontos distintos.
Passo 1
Primeiro precisamos achar o vetor tangente de que é o determina a direção da reta tangente.
A reta tangente é horizontal quando esse vetor só tem componente horizontal, ou seja,
Resolvendo a segunda equação vamos achar
Repara que nenhum desses valores vão fazer a componente do vetor diretor zerar.
Os pontos vão ser aqueles que trocamos esses valores de em
Passo 2
Vamos ver agora quando a reta tangente é vertical, isso acontece quando temos apenas componente vertical, ou seja,
Vamos resolver a segunda equação
Repara que nenhum desses valores vão fazer a componente do vetor diretor zerar.
Os pontos vão ser aqueles que trocamos esses valores de em
Passo 3
Aqui o que ele quer saber é se essa curva é simétrica em relação ao eixo ou ao eixo , para isso vamos ver o valor da curva no oposto, que seria
Repara que mudar o sinal de não muda o valor da componente , mas muda o valor da compoenten então essa curva é simétrica em relação ao eixo .
Passo 4
Aqui ele quer que dada a parametrização da curva, tenhamos as funções que podem ter essa parametrização, ou seja, a relação entre e que dá essa parametrização.
Repara que temos
Da primeira equação vamos ter
Então já podemos perceber que temos duas funções uma com e outra com
Vamos começar achando com
Então
Vamos fazer agora com
Então
Passo 5
O traço é fazer a trajetória dessa curva.
A ideia seria fazer o gráfico de e , mas essas duas funções não são fáceis de fazer, vamos perceber alguns detalhes e com isso ajudar a fazer o gráfico.
A primeira coisa a notar é que vai ser sempre positivo, depois como é uma função polinomial de grau impar, então ele vai de até
A curva “começa” no e e “termina” no e
Repara que
Ou seja
As raízes das duas são iguais, descobrir as raízes não vai ser algo difícil
Já sabemos as raízes.
vamos ver como é a velocidade dessa parada.
A velocidade vai ser
Repara que se o componente vai ser sempre positivo, ou seja, começa em e vai sempre para direita.
Agora vamos com calma, temos dois pontos que são as raízes, sabemos onde “começa” e onde “termina” a função. Se a função “começa” no zero e tem duas raízes ela vai fazer um mínimo em algum lugar entre as raízes, e depois vai seguir para .
Como as funções e são iguais só mudando o sinal isso vai acontecer também com só que dessa vez ele vai ter um máximo entre as raízes.
A última coisa para descobrir agora é onde a velocidade começa a fazer a mudança de sentido. Já vimos como é o sentido da velocidade em vamos ver em
Vamos ter que analisar seu sinal repara que
Isso porque a raízes disso já vimos lá em cima, e sabemos que é uma função de segundo grau com o coeficiente em maior que .
Isso nos diz que a velocidade em começa para baixo depois para baixo e para direita até o ponto depois ele vai para cima e para direita, passa pela raiz e vai para o infinito. A função vai ser igual com sinal todo trocado, então o gráfico vai ficar
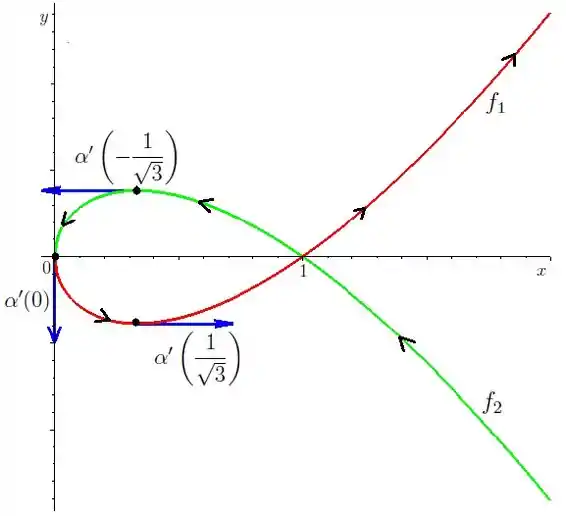
Resposta
- Simétrico em relação a