UnB, Sem Campus, Cálculo 2, P1 - 2008.2, Questão 2b
Considera-se a área entre a curva e o eixo para .
b) Determinar o volume do sólido de rotação, girando-se
b1) em torno da reta b2) em torno da reta
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o volume do sólido de rotação quando a nossa área gira em torno da reta e quando gira em torno da reta .
Nos dois casos, nós vamos usar o método dos anéis para calcular o volume de rotação, onde o volume é dado pela equação:
Onde é o raio externo e o raio interno.
Quando gira em torno de , é como se tivéssemos um raio externo indo da curva até e um raio interno que vai do eixo () até . Já quando a curva gira em torno de , nós temos um raio interno de até o eixo e um raio externo de até . Mas calma que vai ficar mais claro quando a gente olhar os gráficos nos passos.
Vamos lá!
Passo 2
Vamos começar calculando o volume gerado pela rotação da área (em amarelo) em torno da reta :
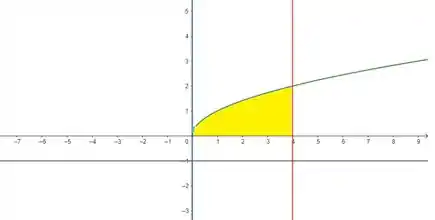
A reta é essa aí em cinza e é em torno dela que a região em amarelo vai rotacionar e gerar um sólido. O volume desse sólido vai ser dado por:
Onde é o raio externo, que vai de até e é o raio interno que vai de a , ou seja:
Substituindo na integral, e sabendo que nosso intervalo de integração vai de a (dados no enunciado), temos:
Elevando ao quadrado:
Integrando, temos:
Aplicando os intervalos de integração:
E temos nosso volume:
Passo 3
Agora nossa área vai girar em torno da reta (em laranja):
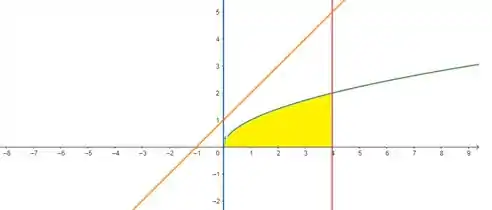
Então, agora nosso raio externo vai de até e nosso raio interno, , vai de até o eixo , ou seja:
Substituindo na integral de volume, temos:
Elevando ao quadrado:
Integrando, temos:
Aplicando os intervalos de integração:
E temos nosso volume:
Valeu, galera! Até a próxima! 😉