Tendo em vista a área entras as funções abaixo:
Calcule o volume do sólido obtido na rotação dessa região em torno do eixo .
Passo 1
Plotei o negócio todo, agora vamos olhar qual é a região:
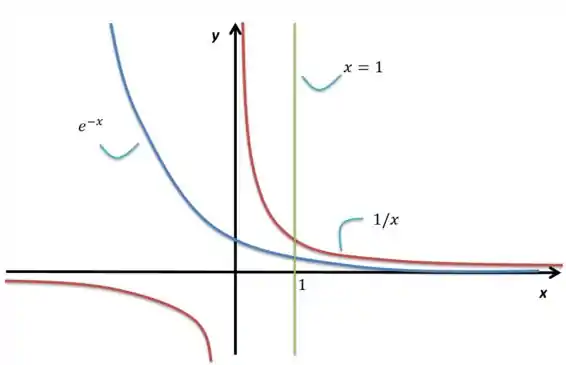
Se você reparar, não existe uma área perfeitamente definida. Olha o que acontece, antes do você tem uma região na qual os gráficos vermelho e azul vão se separando e não tem um “teto” para fechar essa área. Indo para o outro lado, os dois gráficos também não são limitados por uma parede, mas pelo menos eles estão se encostando, diminuindo a área.
O que faremos nesse caso? Vamos calcular o volume de rotação de uma área ilimitada!
Bizarro, eu sei. Não faz nenhum sentido a primeira vista, mas matematicamente é perfeitamente normal. O detalhe é que vamos cair em uma amada integral imprópria.
Passo 2
Bom, se essa área roda em torno de , podemos defini-la assim:
Agora, é só resolver!
Só te recordando, como a integral é imprópria, eu devo fazer um limite para o infinito de uma variável que eu colocarei no lugar do limite superior.
As duas funções de ali vão ficando pequenas no infinito. Ambas tendem a (basta substituir o valor para ter uma noção). Dessa forma, o resultado é aquilo que sobrou de constante: