UNICAMP – Sem campus – Cálculo I – P3 – 2022.1 6º Diurno – 5a
Seja a região R limitada pelas curvas e .
a) Esboce R e calcule sua área
b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.
Passo 1
Fala aí turminha, tudo bem? Vamos detonar essa questão! Começando pelo item a), vamos esboçar a curva . Pra esse tipo de função (radical de grau impar), temos esse formato:
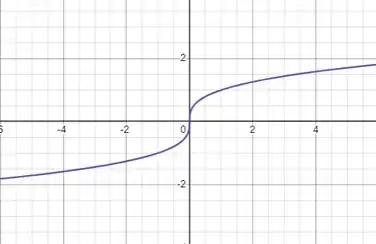
E pra segunda curva descrita é bem tranquilo, . Nela, desenhamos só uma reta na origem:
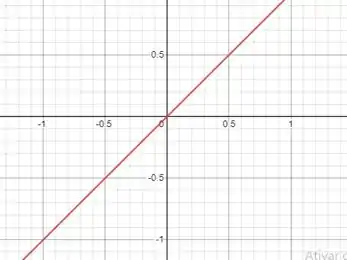
Passo 2
Passo 3
Prontinho. Agora vocês conseguem imaginar como ficaria com as duas funções juntas? Vou mostrar pra vocês:
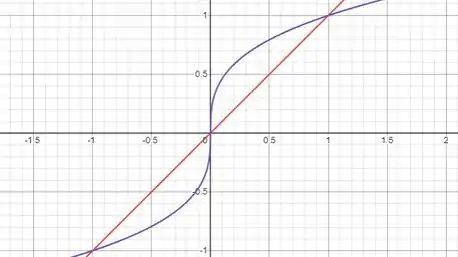
E essa é justamente a região que a questão pede pra gente esboçar. Mas tá faltando uma coisa, precisamos achar os pontos em que as funções se encontram. Tudo bem que na imagem dá pra perceber que é e hahahahaha. Mas em um caso de prova, como você calcularia? Vou mostrar no próximo passo.
Passo 4
Pra gente achar os pontos onde elas se tocam, precisamos igualar as duas funções. Temos portanto:
Resolvendo:
Ou,
E são justamente esses os pontos onde elas se encontram.
Passo 5
Pra calcularmos a área, usaremos o método da integral da subtração das funções. Função que está em “cima” menos a função que está em “baixo”. Mas nossa função aqui tem dois momentos, um em que está em cima, que seria essa área:
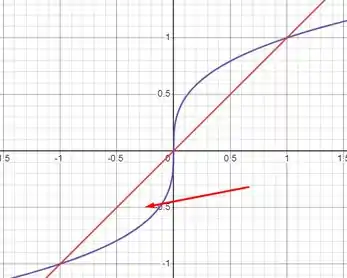
E somariamos com o caso em que a curva está em cima, que é essa área apontada pela seta:
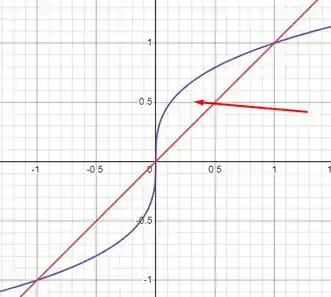
Mas, pra facilitar a nossa vida também podemos partir da seguinte observação: Note que as duas áreas são simétricas entre si. Logo, se a gente calcular a área de uma, vai ser igual a área da outra. Portanto a nossa área total vai ser a área de uma das regiões, multiplicado por 2. Logo, calculando da segunda região, temos que:
Resolvendo
Logo a área da região é: