Considere a região delimitada pelas curvas
a) Calcule a área da região
b) Calcule o volume do sólido obtido pela rotação da região em torno da reta .
Passo 1
Para começar, vamos identificar que região é essa que estamos trabalhando.
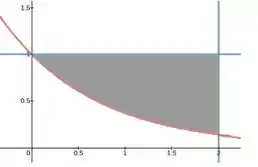
Onde é a reta verde, a reta azul, e a vermelha.
Passo 2
a) Bom, agora para escrever a integral que vai nos dar essa área cinza, fazemos a integral da função de cima, menos a debaixo, afinal, devemos lembrar que para o cálculo de uma área abaixo da função, calculanos a integral da mesma num determinado intervalo, certo? No entanto, não queremos toda área abaixo de , mas sim a área abaixo de, menos a área abaixo da função vermelha . Temos então:
Tranquilinho, né? Precisamos lembrar ainda que estamos procurando a integral quando o x varia entre
Passo 3
b) Para calcular o volume, precisamos antes fazer uma análise na área:
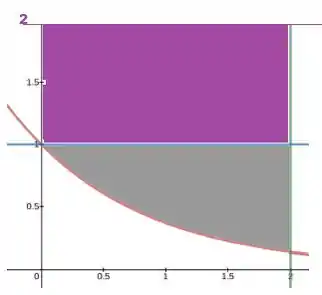
Se nós fizéssemos o cálculo do volume girando tem torno do y=2, teríamos o volume dessa área toda (cinza + roxa) sendo rotacionada, e não é o que queremos.
Então, ao aplicar a fórmula, ao invés de termos:
Lembrando que esse surge a partir da fórmula do cálculo de volume a partir de uma rotação, tranquilo?
Vamos na realidade ter:
A nova parcela que apareceu na integral representa a remoção da área roxa da parte a ser rotacionada. Tranquilo?
Passo 4
Bora resolver aí essa integral então.