Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Volumes de Sólidos Infinitos

Ver Teoria
Exercício 312456789101112131415161718192021

Enunciado

Ao rotacionarmos em torno do eixo x a região delimitada pela função f x = e - x ,   0 ≤ x ≤ α , obtemos um sólido conhecido por Trombeta de Gabriel. No entando, ao girarmos em torno do eixo y , obtemos um outro sólido conhecido como Vulcão de Descartes.

b Calcule o volume do Vulcão de Descartes, para α suficientemente grande, ou seja, α → ∞ .

Passo 1

b Nosso esboço é o mesmo da última questão para um α qualquer.

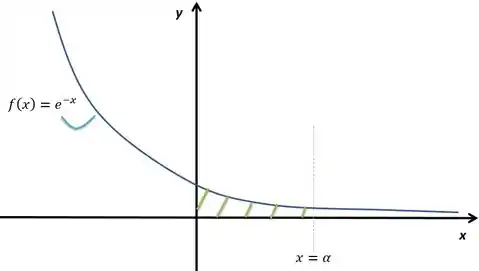
Rotacionando em torno do eixo y nós teríamos o seguinte, pelo método das cascas cilíndricas:

V = ∫ 0 α 2 π r x h x d x = ∫ 0 α 2 π x e - x d x

Vamos resolver essa integral para um α qualquer e depois fazemos ele tender a ∞ .

Passo 2

Vamos com a integral por partes. Pelo LIATE, a o u = x e o d v = e - x d x :

u = x → d u = d x

d v = e - x d x → v = - e - x

∫ 0 α 2 π x e - x d x = 2 π - x e - x + ∫ e - x d x [ α 0

= 2 π - x e - x - e - x [ α 0

= 2 π - α e - α - e - α - 2 π - 0 e 0 - e 0

2 π - α - 1 e α + 1 = 2 π - α - 1 + e α e α

Ok, agora calculamos o limite disso aí quando α vai a + ∞ .

Passo 3

lim α → ∞ ⁡ 2 π - α - 1 + e α e α

Substituindo esse limite aí a gente cai numa indeterminação - ∞ ∞ . Vamos de L’Hospital então:

lim α → ∞ ⁡ 2 π - α - 1 + e α e α → L ' H lim α → ∞ ⁡ 2 π - α - 1 + e α ' e α '

= lim α → ∞ ⁡ 2 π - 1 + e α e α = lim α → ∞ ⁡ 2 π - 1 e α + 1

= 2 π - 1 ∞ + 1 = 2 π

Esse é o volume que estávamos procurando!

Resposta

V = 2 π   u . v .

Exercícios de Livros Relacionados

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = 9 - x 2 ; y = 0
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = e 3 x 1 + e 6 x ; y = 0 ; x = 0 ; x = 1
Encontre o volume do sólido cuja base é a região delimitada pela curva x = 1 - y 2 e o eixo y e cujas seções transversais, tomadas perpendicularmente ao eixo y , são quadrados.
Calcule o volume do sólido cuja base é o semicírculo 4x²+y²
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.