Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Volumes de Sólidos Infinitos

Ver Teoria
Exercício 141234567891011121315161718192021

Enunciado

UNICAMP – Sem campus – Cálculo 2 – P2 – 5º tarde - 4

Determine o volume do sólido entre as esferas x 2 + y 2 + z 2 = 1 e x 2 + y 2 + z 2 = 4 e no interior da região cônica z 2 ≥ x 2 + y 2 .

Passo 1

Fala turminha, tudo em cima? Bora lá resolver essa questão. Primeiro, vamos atrás de desenhar essa nossa figura que é formada por uma esfera de raio 2, esfera de raio 1 e um cone. Fica da seguinte forma:

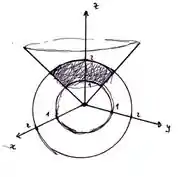
De forma que nossa integral fique seja:

V = ∫ ∫ ∫ d V R

Que podemos reescrever trocado as coordenadas cartesianas por esféricas, fazendo a seguinte substituição:

x = r   s e n   ( θ )

y = r cos ⁡ ( θ )

z = r d ϕ

d x d y d z = r   d r   d θ d ϕ

Obtendo por sua vez:

V = ∫ ∫ ∫ d V R = ∫ ∫ ��� r 2 s e n θ d r d θ d ϕ

Passo 2

Pra gente montar a nossa integral, precisamos primeiro os limites de integração (delimitado pelos raios das esferas). Primeiro o d ϕ representa toda a volta em um círculo. Dentro de uma integral, entendemos isso como de 0 a 2 π . Portanto:

∫ 0 2 π d ϕ

Para o cone, ele é representado no eixo y dada pela abertura geral de cones: de 0 a π 4 . E dentro dos raios, os limites de integração vão ser dados pela diferença do raio das duas esferas, ou seja: de 1 (raio da esfera menor) a 2 (raio da esfera maior). Nossa integral portanto fica com cara:

∫ 0 2 π d ϕ ∫ 0 π 4 s e n   θ ∫ 1 2 r 2 d r

Passo 3

Portanto, nosso volume vai ser dado por:

V = ∫ 0 2 π d ϕ ∫ 0 π 4 s e n   θ ∫ 1 2 r 2 d r

Resolvendo as integrais triviais:

∫ 0 2 π d ϕ = 2 π - 0 = 2 π

∫ 0 π 4 s e n   θ =   - c o s θ ​ 0 π 4 =   - cos ⁡ π 4 - cos ⁡ 0

= - 2 2 - 1

∫ 1 2 r 2 d r = r 3 3 ​ 1 2

= 2 3 3 - 1 3 3 = 7 3

Logo, multiplicando tudo:

V = 7 2 - 2 π 3   u . v

Resposta

V = 7 2 - 2 π 3   u . v

Exercícios de Livros Relacionados

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = 9 - x 2 ; y = 0
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = e 3 x 1 + e 6 x ; y = 0 ; x = 0 ; x = 1
Encontre o volume do sólido cuja base é a região delimitada pela curva x = 1 - y 2 e o eixo y e cujas seções transversais, tomadas perpendicularmente ao eixo y , são quadrados.
Calcule o volume do sólido cuja base é o semicírculo 4x²+y²
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.