Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Volumes de Sólidos Infinitos

Ver Teoria
Exercício 712345689101112131415161718192021

Enunciado

f x = 1 x - 1 x 2 , cujo gráfico está esboçado abaixo:

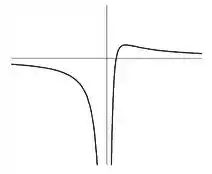
Sabendo que o eixo x é uma assíntota horizontal do gráfico de f , faça o que se pede.

  1. Seja R a região plana definida por

    2. R = x ,   y ∈ R 2 0 ≤ y ≤ f ( x )

    Calcule a área de R e conclua que ela é infinita.

  2. Seja S o sólido obtido pela rotação da região R em torno do eixo x . Calcule o volume de S .

Passo 1

a) Queremos calcular uma área do R 2 e ja aprendemos que isso pode ser feito por meio de uma integral definida, só precisamos saber o interval de integração. Esse intervalo foi dado pela condição R = x ,   y ∈ R 2 0 ≤ y ≤ f ( x )

Show, mas como que eu interpreto essa parada? Bom, basicamente o que essa condição ta dizendo é que todos os y da região R estão contidos entre 0 e o gráfico de f . Em outras palavras, ela ta dizendo que a área de R está na região abaixo do gráfico de f até o eixo x (eixo em que y = 0 ) .  

Só que ainda tem mais um problema. Perceba que a condição define um intervalo referente à variável y e precisamos de um intervalo de integração referente à x , já que a função está nessa variável. E aí, o que fazer agora?

Bom, já que o intervalo dado começa em y = 0 é só descobrir quanto vale x nesse ponto e teremos o limite de integração inferior.

f x = 0 ↔ 1 x - 1 x 2 = 0 ↔ x - 1 x 2 = 0 ↔ x = 1

O limite superior vai ser + ∞ , porque não foi dado um valor de y final.

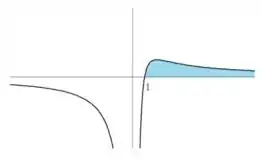Portanto, a área que queremos calcular pode ser esboçada da seguinte maneira:

Passo 2

Agora é só montar a integral e calcular!

Á r e a   d e   R =   ∫ 1 + ∞ 1 x - 1 x 2   d x

Como é uma integral com limite superior infinito temos que transformar em um limite:

Á r e a   d e   R =   lim b → + ∞ ⁡ ∫ 1 b 1 x - 1 x 2   d x  

  lim b → + ∞ ⁡ ln ⁡ x + 1 x 1 b = lim b → + ∞ ⁡ ln ⁡ b + 1 b - ( 0 + 1 ) = lim b → + ∞ ⁡ ln ⁡ b + 1 b - 1

Como

l i m b → + ∞ ln ⁡ b = + ∞

E

l i m b → + ∞ 1 b = 0

Temos que

Á r e a   d e   R = + ∞

Passo 3

b) Existem diferentes maneiras de calcular o volume desse sólido S gerado pela rotação de R . Nesse caso vamos usar o método dos discos. Primeiro, note que rotacionando a área R em torno do eixo x teremos um sólido que começa em x = 1 e se extende infinitamente na direção do eixo x . Lembrando que uma integral é uma maneira de calcular mais facilmente a soma de infinitas partes, vamos dividir o sólido em vários discos perpendiculares ao eixo x e com r a i o = f ( x ) . A soma da área de cada disco gerado dará o volume do sólido. Escrevendo tudo isso que falamos em “matematiquês” temos:

v o l S =   ∫ 1 + ∞ A ( x )   d x

Onde A ( x ) é a área de cada disco de raio f ( x ) , ou seja

A x = π f x 2 = π 1 x - 1 x 2 2

Voltando pra integral:

v o l S =   ∫ 1 + ∞ π 1 x - 1 x 2 2   d x

Passo 4

Agora temos só que resolver a integral. Primeiro vamos transformá-la em um limite.

  ∫ 1 + ∞ π 1 x - 1 x 2 2   d x = lim b → + ∞ ⁡ ∫ 1 b π 1 x - 1 x 2 2   d x

Resolvendo temos:

lim b → + ∞ ⁡ ∫ 1 b π 1 x - 1 x 2 2   d x = lim b → + ∞ ⁡ ∫ 1 b π 1 x ² - 2 x 3 + 1 x 4 d x = lim b → + ∞ ⁡ π - 1 x + 1 x 2 - 1 3 x 3 1 b = π lim b → + ∞ ⁡ - 1 b + 1 b 2 - 1 3 b 3 - - 1 + 1 - 1 3 = π 0 - - 1 3 = π 3

Resposta

a) + ∞

b) π 3

Exercícios de Livros Relacionados

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = 9 - x 2 ; y = 0
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = e 3 x 1 + e 6 x ; y = 0 ; x = 0 ; x = 1
Encontre o volume do sólido cuja base é a região delimitada pela curva x = 1 - y 2 e o eixo y e cujas seções transversais, tomadas perpendicularmente ao eixo y , são quadrados.
Calcule o volume do sólido cuja base é o semicírculo 4x²+y²
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.