Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Volumes de Sólidos Infinitos

Ver Teoria
Exercício 151234567891011121314161718192021

Enunciado

UNICAMP – Sem campus – Cálculo II – P3 – 2022.1 6º Noturno – 5a

Seja R a região limitada pelas curvas y = 2 x 2 + x e y = 3 x

a) Esboce R e calcule a sua área.

b) Calcule o volume do sólido gerado pela rotação de R em torno do eixo x.

Passo 1

Fala aí turminha da UNICAMP, tudo bem? Vamos detonar essa questão! Começando pelo item a), vamos esboçar a curva y = 2 x 2 + x . Nela, sabemos que é uma parábola, com concavidade para cima (constante que acompanha o x 2 é positiva). A partir disso, a gente pode desenhar ela da seguinte forma:

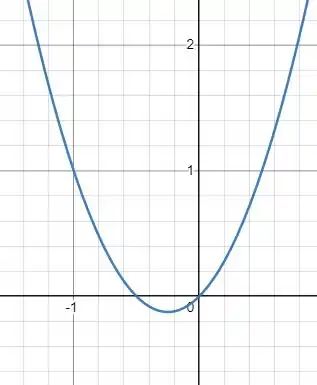
Passo 2

Show, agora vamos pra segunda curva. Ela é em tranquila porque é descrita apenas por uma reta y = 3 x . No gráfico, ela é representada por:

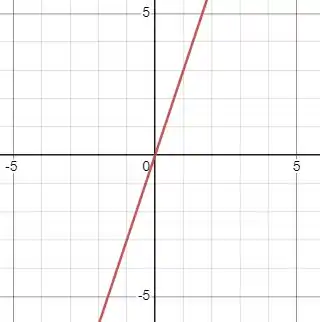
Passo 3

Prontinho. Agora vocês conseguem imaginar como ficaria com as duas funções juntas? Vou mostrar pra vocês:

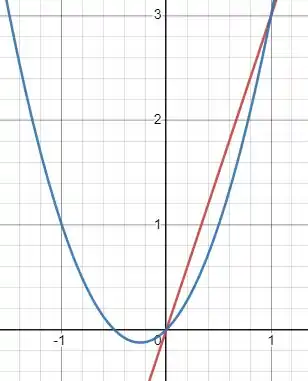
E essa é justamente a região que a questão pede pra gente esboçar. Mas tá faltando uma coisa, precisamos achar os pontos em que as funções se encontram. Tudo bem que na imagem dá pra perceber que é x = 1 hahahahaha. Mas em um caso de prova, como você calcularia? Vou mostrar no próximo passo.

Passo 4

Pra gente achar os pontos onde elas se tocam, precisamos igualar as duas funções. Temos portanto:

2 x 2 + x = 3 x

2 x = 2

x = 1

Agora, bora cair pro cálculo da área! Pra calcularmos a área, usaremos o método da integral da subtração das funções. Função que está em “cima” menos a função que está em “baixo”. Logo,

∫ 0 1 ( 3 x - ( 2 x 2 + x ) ) d x

Resolvendo-a, temos que:

2 x 2 2 - 2 x 3 3 ​ 0 1 = 1 3

Logo a área da região é de:

R = 1 3   u . a

Resposta

R = 1 3   u . a

Exercícios de Livros Relacionados

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = 9 - x 2 ; y = 0
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = e 3 x 1 + e 6 x ; y = 0 ; x = 0 ; x = 1
Encontre o volume do sólido cuja base é a região delimitada pela curva x = 1 - y 2 e o eixo y e cujas seções transversais, tomadas perpendicularmente ao eixo y , são quadrados.
Calcule o volume do sólido cuja base é o semicírculo 4x²+y²
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.