Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Volumes de Sólidos Infinitos

Ver Teoria
Exercício 612345789101112131415161718192021

Enunciado

  1. Seja C a região do plano delimitada superiormente pelo gráfico de f x = 1 a + x , à esquerda por x = 1 e inferiormente pelo eixo x . Seja V o volume do sólido gerado pela rotação de C em torno do eixo x . Então:
  1. V é finito para todo a > 0 .
  2. V não é finito para nenhum a > 0 .
  3. V é finito apenas para a > 1 .
  4. V é finito apenas para 0 < a < 1 .

Passo 1

Bem, a primeira coisa aqui é desenhar a região C ...

A curva de f x = 1 a + x é uma curva semelhante a 1 / x . Mas deslocada de a unidades a esquerda em x ...

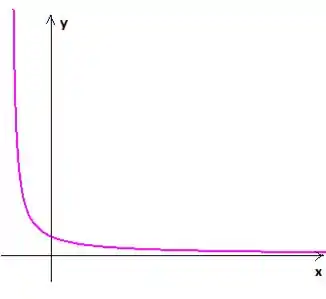
A região está abaixo dessa curva até o eixo x e delimitada também pela reta vertical x = 1 ...

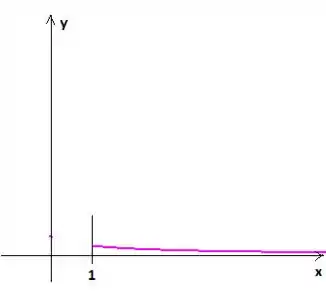
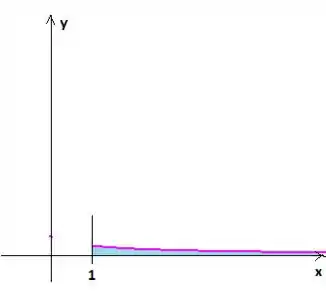
Passo 2

Quando giramos essa região C ao redor do eixo x determinamos um sólido só que esse sólido é infinito, saca? O problema quer saber justamente para quais intervalos de a , o volume converge para algum valor, ou seja, exista volume finito. Para isso, vamos usar a expressão do cálculo do volume pelo método dos discos (pois estamos girando ao redor de x ) :

V = ∫ a b π f x 2 d x

Onde a e b são os limites do sólido em x , ou seja, a é onde começa, no 1 , e b onde “termina”, no infinito positivo nesse caso...

V = ∫ 1 + ∞ π f x 2 d x

A função f x é justamente a curva que estamos girando, no caso a curva...

f x = 1 a + x

Passo 3

Calculando essa integral...

V = ∫ 1 + ∞ π 1 a + x 2 d x

Essa integral é pela definição, é um limite...

lim t → + ∞ ⁡ ∫ 1 t π 1 a + x 2 d x

A integral

π ∫ 1 t 1 x + a 2 d x

Podemos calcular:

π ∫ 1 t 1 x + a 2   d x =

π - 1 x + a 1 t =

Substituindo os limites de integração...

π - 1 t + a - - 1 1 + a = π 1 1 + a - 1 t + a

Passo 4

Aplicando o limite no resultado da integral...

lim t → + ∞ ⁡ ∫ 1 t π 1 x + a 2 d x = lim t → + ∞ ⁡ π 1 1 + a - 1 t + a =

Ora, por propriedades de limites...

lim t → + ∞ ⁡ π 1 + a - lim t → + ∞ ⁡ π t + a =

O primeiro limite é uma constante e quando x vai ao infinito ele não se altera, portanto...

π 1 + a - lim t → + ∞ ⁡ π t + a =

Já esse outro...

π 1 + a - lim t → + ∞ ⁡ π t + a = π 1 + a - 0

Logo...

lim t → + ∞ ⁡ ∫ 1 t π 1 x + a 2 d x = π 1 + a

Passo 5

Então o volume é

V = ∫ 1 + ∞ π 1 a + x 2 d x = π 1 + a

Veja que a integral é convergente e converge para o valor finito do volume para qualquer valor de a , tirando a = - 1 , logo a resposta correta é...

  1. V é finito para todo a > 0 .

Resposta

  1. V é finito para todo a > 0 .

Exercícios de Livros Relacionados

Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = 9 - x 2 ; y = 0
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo x . y = e 3 x 1 + e 6 x ; y = 0 ; x = 0 ; x = 1
Encontre o volume do sólido cuja base é a região delimitada pela curva x = 1 - y 2 e o eixo y e cujas seções transversais, tomadas perpendicularmente ao eixo y , são quadrados.
Calcule o volume do sólido cuja base é o semicírculo 4x²+y²
Um certo sólido tem uma altura de 1m e uma seção transversal, tomada x metros acima da base do sólido, é uma região anular de raio interno x 2m e raio externo xm . Encontre o volume do sólido.