UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo de Várias Variáveis - Lista 2 - Integral de Linha, Questão 2.2.10
Um arame tem a forma da curva interseção do hemisfério , , com o plano e a densidade no ponto é . Qual a massa do arame?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a massa do arame de densidade , sabendo que ele tem o formato da curva de interseção de um hemisfério da esfera , , com o plano . É como se o nosso arame fosse essa partizinha vermelha da esfera destacada pelo plano em amarelo:
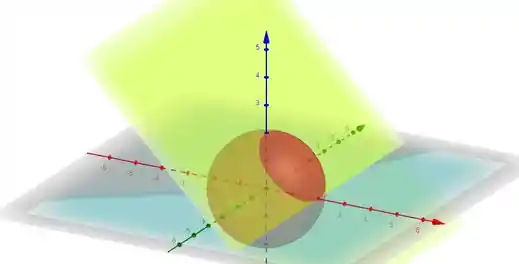
Pra calcular a massa dele, vamos precisar calcular a integral da função densidade sobre a curva :
Como essa é uma integral de linha sobre uma curva, o que vamos fazer é tentar parametrizar essa curva, definindo os limites de integração e escrever a densidade em função da parametrização. Integrando, teremos nossa massa .
Vamos lá!
Passo 2
Como queremos a curva de interseção das superfícies e , vamos isolar na equação do plano e substituir uma equação na outra:
Substituindo em :
Completando o quadrado, vamos ter:
Dividindo todo mundo por :
E temos a equação de uma esfera no plano, que nós podemos parametrizar usando:
E
Para descobrir a coordenada , vamos usar novamente a equação do plano:
E temos nossa parametrização:
Como varia de a , substituindo na parametrização da coordenada , obtemos:
Passo 3
Vamos agora calcular o módulo da derivada desse vetor, que será o nosso e nós vamos precisar para calcular a integral de linha. Primeiro, derivando, temos:
Pra calcular o módulo, nós tiramos a raiz quadrada das coordenadas do vetor ao quadrado. Fica assim:
Usando a identidade trigonométrica , temos:
Passo 4
A nossa função densidade é dada por . Então, usando a parametrização e , vamos ter:
Usando a identidade , temos:
Passo 5
Voltando pra nossa integral de linha e substituindo tudo, temos:
Colocando o produto das constantes do lado de fora da integral:
Integrando em relação a :
Aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉