UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo de Várias Variáveis - Lista 2 - Integral de Linha, Questão 2.2.9
Um arame tem o formato da parte da elipse situada no primeiro quadrante e a densidade no ponto é . Qual a massa do arame?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a massa do arame de densidade , sabendo que ele tem o formato de parte da elipse situada no primeiro quadrante. É como se o nosso arame fosse essa curvinha aí:
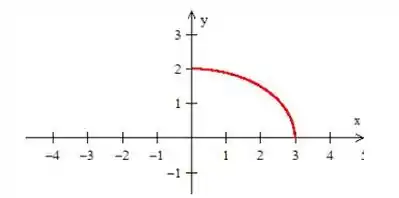
Pra calcular a massa dele, vamos precisar calcular a integral da função densidade sobre a curva :
Como essa é uma integral de linha sobre uma curva, o que vamos fazer é tentar parametrizar essa curva, definindo os limites de integração e escrever a densidade em função da parametrizar. Integrando, teremos nossa massa .
Vamos lá!
Passo 2
Galera, no geral, uma elipse do tipo:
Tem uma parametrização do tipo:
Esse intervalo significa que a elipse dá uma volta completa. No nosso caso, a elipse encontra-se apenas no primeiro quadrante, então varia no intervalo . Além disso, podemos escrever a equação da elipse na forma:
Então, e . Assim, temos a parametrização:
Ou seja, . Derivando esse vetor, vamos ter:
Passo 3
A nossa função densidade é dada por . Então, usando a parametrização e , vamos ter:
Passo 4
Devemos agora encontrar o termo , tirando o móduto de :
E o módulo de um vetor é dado pela raiz quadrada da soma de suas coordenadas ao quadrado, ou seja, para , temos:
Passo 5
Voltando pra nossa integral de linha e substituindo tudo, temos:
Lembrando que , vamos ter:
Passo 6
Pra facilitar um pouco nossa vida nessa integração, vamos fazer uma substituição do tipo:
Não podemos esquecer dos limites:
Assim, nossa integral vai ficar:
Integrando em relação a :
Aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉