Um fio delgado tem a forma de reta que une os pontos e . Determine o momento de inércia em relação à reta , supondo que a densidade no ponto é proporcional à distância do ponto ao eixo .
Passo 1
Momento de inércia não tem erro, vamos usar a fórmula que vimos lá na teoria:
Só que aqui a reta é , vamos ver como que fica isso graficamente:
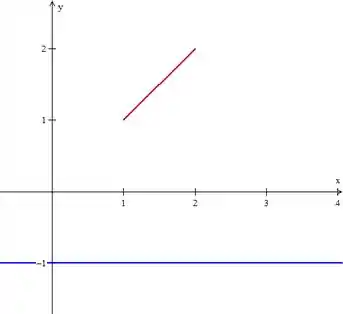
Aqui, dá pra ver que a distância do de um ponto no segmento (em vermelho) e e reta (em azul) é, simplesmente, sua coordenada , ou seja, a fórmula fica:
Que a gente sabe calcular pela fómula da integral de linha:
Agora vamos parametrizar a curva e encontrar esse densidade aí pra que possamos calcular a integral!
Passo 2
O segmento é bem tranquilo de parametrizar:
E o módulo do vetor normal fica:
Passo 3
A densidade também não é nada muito elaborado, ele diz que é proporcional a distância ao eixo , então simplesmete vamos ter:
Usando aquela paramentrização que vimos no passo anterior, a gente fica com algo assim:
Agora á só calcular a integral!
Passo 4
Substituindo tudo na nossa fórmula lá do passo 1, a gente vai ter:
Então é isso, pronto!