Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 71234568910111213141516171819202122232425

Enunciado

  1. Calcule o momento de inércia de um fio retilíneo homogêneo de comprimento L , em torno de um eixo perpendicular ao fio e passando por uma das extremidades do fio, em função de sua massa.

Passo 1

Momento de inércia de um fio em relação a uma perpendicular ( I P )? Sim, neh! então vamos usar uma integral de linha, aliás, uma não a integral de linha

I P = ∫ C   r 2 δ x ,   y d s

Onde r é a distância e cada ponto até ao eixo de referência perpendicular P (vamos falar melhor dele já já ) e δ x ,   y é a densidade da curva que para nossa alegria é uma constante (fio homogêneo). Logo...

I P = k ∫ C   r 2 d s

Mas o mais importante agora é saber que em integral de linha como essa sempre devemos seguir um passo a passo maroto:

  1. Parametrizar a curva
  2. Trocar os termos da função pelos da parametrização
  3. Encontrar o termo d s

Bora?! :D

Passo 2

Devemos parametrizar a curva C , mas antes de tudo quem é essa curva que estamos trabalhando?

Ora! O próprio problema nos disse que é um fio retilíneo. Então é um pedacinho de reta que pra facilitar, vamos desenha-lo no plano cartesiano em cima do eixo y :

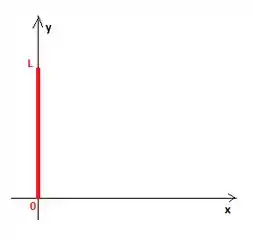
Como esse fio está em cima do eixo y , o x é fixo e vale x = 0 . Então uma boa parametrização para essa retinha é deixar o y móvel

y = t

e o x , como já comentamos...

x = 0

Logo, arrumando essa parametrização aí de uma forma mais elegante...

r t = 0 ,   t

Podemos perceber que o fio tem y variando de 0 até a altura L máxima. Como y = t ...

0 ≤ t ≤ L

Passo 3

Então, a nossa próxima tarefa é agora trocar os termos da função que estamos integrando (no caso é r 2 ) pelos termos da parametrização.

Bem, como já comentamos, r é a distância dos pontos ao eixo de referência. Com a linha dessa forma

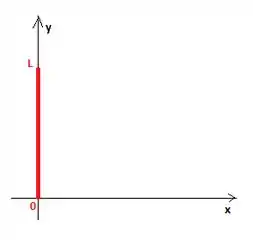
podemos pegar o eixo x para ser o eixo de referência, afinal de contas ele é perpendicular ao fio e passa por uma de suas extremidades, sacou?

Então, o r nesse caso é igal a y (distância até ao eixo x ):

r = y

como y = t ...

r = t

Passo 4

Devemos agora encontrar o termo d s fazendo

d s = r ' t d t

derivando a curva portanto...

r t = 0 ,   t →       r ' t = 0 ,   1

extraindo o módulo desse vetor derivada...

r ' ( t ) = 0 2 + 1 2 =

1

d s = d t

Passo 5

Finalmente então, precisamos retornar à integral de linha que estamos trabalhando

I P = k ∫ C   r 2 d s

e substituir todos os caras que falamos até agora obtendo:

I x = k ∫ C   r 2 d s = k ∫ 0 L t 2 d t

resolvendo essa integral aí:

I x = k t 3 3 0 L =

k L 3 3

Passo 6

Mas espera! Embora calculamos o momento de inércia pedido, o problema nos pede em função da massa M , então precisamos encontra-la!

Não se preocupe, pois massa de um fio é outra integral de linha, mas dessa vez...

M = ∫ C   δ x ,   y d s

Como a função densidade é uma constante k ...

M = k ∫ C   d s

Pow!!! Integral de linha de 1 d s é o... comprimento do fio ! Como o comprimento do nisso lio é L ...

M = k L

Você encontra o mesmo resultado se você resolver a integral de linha substituindo os caras que encontramos:

M = k ∫ C   d s = k ∫ 0 L d t

Então o momento de inércia em função da Massa é:

I x = k L 3 3 = k L L 2 3 =

M L 2 3

Resposta

M L 2 3

Exercícios de Livros Relacionados

(a) Escreva fórmulas semelhantes à Equação 4 para o centro de massa x C M ,y C M ,z C M de um arame fino com função densidade ρ x ,y ,z e forma da curva espacial C .(b) Determine o centro de massa de
Determine a massa e o centro de massa de um arame com formato da hélice x = t, y = cos ⁡ t, z = s e nt, 0 ≤ t ≤ 2 π, se a densidade em qualquer ponto for igual ao quadrado da sua distância do ponto à
Use o Exercício 22 para encontrar o centroide da região triangular de vértices 0,0 ,( a , 0 ) e ( a , b ) , onde a0 e b0 .
Determine a massa e o centro de massa de um arame fino no formato de um quarto de círculo x 2 + y 2 = r 2 , x ≥ 0 , y ≥ 0 , se a função densidade for ρ x , y = x + y
Dado um arame semicircular uniforme de raio 4 cm.Mostrar que o momento de inércia em relação ao diâmetro que passa pelos extremos do arame 8 M , sendo M a massa do arame.