USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 22
Determine a massa e o centro de massa do sólido limitado pelo paraboloide e pelo plano , se tem densidade constante .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a massa e o centro de massa do sólido que é limitado pelo paraboloide e pelo plano , sabendo que o sólido tem densidade constante . Vamos primeiro dar uma olhadinha no gráfico dessa região:
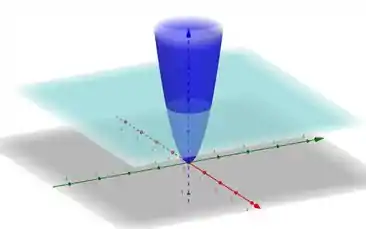
Observe que o plano em azul claro é o plano , que a gente não sabe o valor ao certo, mas sabe que ele é positivo. Então, ele pode tá em qualquer lugar ali em cima do plano , de qualquer forma, a gente já consegue ter uma ideia de como é a região do sólido que a gente tá analisando.
Pra nos ajudar a definir essa região, vamos usar as coordenadas cilíndricas através das relações:
Em seguida, vamos calcular a massa do nosso sólido por meio da integral tripla:
Onde é a nossa região de integração e é a função densidade, que no nosso caso é a constante . De forma parecida, vamos calcular as coordenadas do centro de massa do sólido usando as equações:
Onde , e são os momentos de inércia do sólido em relação aos três planos coordenados. Mas como o parabolóide é cilíndrico em volta do eixo e tem densidade constante, o centro de massa nos eixos e são zero por causa da simetria: . E aí, vamos calcular apenas:
Vamos lá!
Passo 2
Vamos começar convertendo as equações para as coordenadas cilíndricas:
Então, a gente acha a interseção das duas superfícies pra achar o raio máximo:
Sendo assim, nós vamos ter o raio variando em , o ângulo variando no intervalo e a altura do sólido variando em . Usando esses intervalos, montamos nossa integral da massa, com :
Passo 3
Integrando em relação a , temos:
Agora em relação a :
Aplicando os limites de integração em :
Finalmente, integramos em relação a :
Aplicando os limites em :
Temos nossa massa:
Passo 4
Como já sabemos que , vamos calcular apenas o momento de inércia:
Substituindo junto com os mesmos limites de integração do passo anterior, temos:
Integrando em relação a :
Agora integrando em relação a :
Aplicando os limites de integração em :
Finalmente, integramos em relação a :
Aplicando os limites em :
Temos nosso momento de inércia:
Então, observando as equações das coordenadas do centro de massa:
Com , calculado no passo , vamos ter , e
Ou seja, nosso centro de massa é .
Valeu, galera! Até a próxima! 😉