UFF, Sem Campus, Física 1, Listas de Física 1 - Profº Marcos Sergio - Lista 1, Questão 4
Um trem de metrô parte do repouso em uma estação e acelera com uma taxa constante de durante . Em seguida, viaja durante com velocidade constante e depois, reduz a velocidade com uma aceleração constante de até parar na estação seguinte. Calcule a distância total percorrida.
Passo 1
Eaee!!! Belezinha? Bom... primeiramente vamos analisar cada parte do movimento desse trem:
- Primeiramente o trem sai do repouso e acelera a uma taxa constante de num período de ;
- Mantém uma velocidade constante por ;
- Desacelera até o repouso a uma taxa de até para na próxima estação.
Visualmente, temos a seguinte representação:
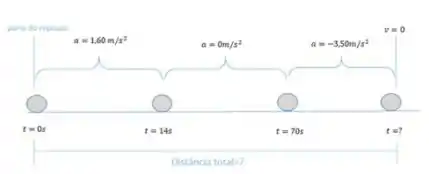
Agora, devemos analisar cada parte para encontrarmos a distância total percorrida utilizando as seguintes equações de movimento:
E
Onde é a distância final, é a distância inicial, é a velocidade inicial, é a velocidade final, é a aceleração e é o tempo!
E aí?? Bora lá??
😉
Passo 2
Assim, para o primeiro trecho, em que o trem está acelerando, temos pela equação da posição em função do tempo:
E sua velocidade ao final dos é dada por:
Passo 3
Para a segunda parte em que a aceleração é constante (ou seja, ), temos:
Passo 4
Para a última parte, em que o trem desacelera até parar, temos que o tempo que ele leva para isso é dado da seguinte forma:
Assim, substituindo os valores, temos:
Assim, a distância que ele percorre até parar é dada por:
Passo 5
Dessa forma, a distância total percorrida pelo trem é dada por:
Entendeu direitinho? Responde aee ;)
