Uma sala tem dimensões de 3,00 metros (altura) 3,70 m 4,30 m. Partindo de um vértice, uma mosca voa aleatoriamente pousando no vértice diagonalmente oposto.
(a) Qual é o módulo de seu deslocamento?
(b) Poderia o comprimento de sua trajetória ser menor do que este módulo?
(c) Maior do que este módulo?
(d) Igual a este módulo?
(e) Escolha um sistema de coordenadas adequado e expresse as componentes do vetor deslocamento em termos dos vetores unitários associados a esse sistema.
(f) Se a mosca caminhar, em vez de voar, qual é o comprimento do menor caminho que ela pode tomar?
(Dica: isto pode ser respondido sem cálculo sofisticado. A sala é como uma caixa. Desdobre as paredes projetando-as sobre um plano.)
Passo 1
Oi tudo bem? Essa questão aprece difícil, mas vou fazer junto com você!
Esse é um problema que envolve a visualização do espaço em três dimensões! E por isso vamos falar em vetores!
Para facilitar, vou representar uma caixa com dimensões e o deslocamento da mosca:
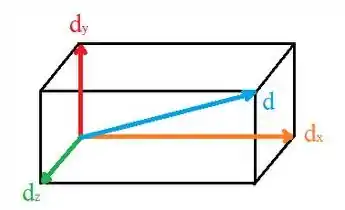
Saindo de um vértice e indo aleatoriamente até o outro, na diagonal oposta, podemos calcular a diagonal desse paralelepípedo e achar o deslocamento da mosca!
Também podemos, com as medidas da caixa, determinar vetores que representam os lados dela e assim responder as outras questões. Mas relaxa, vamos fazer passo a passo
Passo 2
(a) ,(b), (c) e (d):
Utilizando o modelo de caixa do passo anterior, o módulo do deslocamento vai ser aquela diagonal, pois saímos do vértice inferior e chegamos naquele vértice oposto lá em cima na caixa.
As dimensões da caixa são:
E a diagonal de um paralelepípedo é:
Beleza?

E esse seria o menor caminho! Isso porque, considerando que a menor distância entre dois pontos é uma reta, e a distâncias entre as quinas é a diagonal, então a mosca percorreu sim o menor caminho.
Por isso que a distância percorrida pela mosca só pode ser maior ou igual, nunca menor.
Nossa resposta para a letra (b) seria NÃO, (c) seria SIM e (d) SIM
Passo 3
(e)
Agora o problema pede para representar na forma vetorial as dimensões da caixa. Vou resgatar o desenho que fiz no passo 1:
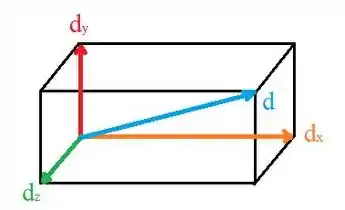
Sabendo que o versor que dá direção e sentido no eixo é = , do eixo é e de é , e usando as dimensões da caixa
Podemos definir um vetor com as dimensões dessa caixa:
Beleza? Vamos para a próxima letra?
Passo 4
(f) agora a mosca vai caminhar! Precisamos pensar no menor caminho possível! A ideia aqui é virar a parede lateral para o chão para encontrar a menor distância entre os dois pontos. Então ela precisa caminhar pelos dois menores lados e depois atravessar até o vértice oposto, assim:
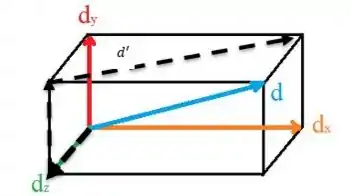
Enxergando da vista superior, temos que é o seguinte:
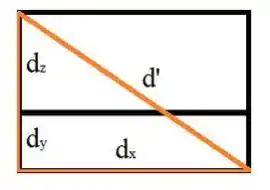
Se você inverter, por exemplo somar ou verá que no final o triângulo retângulo formado será maior e a mosca andará por um caminho maior
Substituindo os valores temos:
E é isso!
Espero ter ajudado!