UFF, Sem Campus, Física 1, Listas de Física 1 - Profº Marcos Sergio - Lista 1, Questão 6a
Um esquiador está deslizando sem atrito sobre uma pista de neve horizontal com velocidade constante de . Subitamente ele começa a descer uma rampa com inclinação de . Na base da mesma, sua velocidade é de .
a) Qual é o comprimento da rampa?
Passo 1
Eaee!!! Belezinha? Bom... vamos analisar a questão pela figura abaixo:
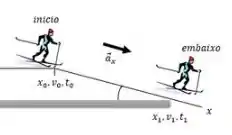
O esquiador tem uma posição, uma velocidade e um tempo inicial (, e , respectivamente) ... que é quando ele começa a descer a rampa.
Ao final da rampa o esquiador tem uma posição, uma velocidade e um tempo final (, e , respectivamente).
Para descobrirmos o tamanho da rampa, podemos utilizar a equação de Torricelli:
Onde é a aceleração com que o esquiador desce a rampa, que é dada por:
Em que é a aceleração da gravidade.
Agora é só aplicação das fórmulas!! Bora lá??
😉
Passo 2
Assim, substituindo os valores na equação de Torricelli, temos:
Que é o tamanho da rampa!!
Entendeu direitinho? Responde aee ;)
