Um motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
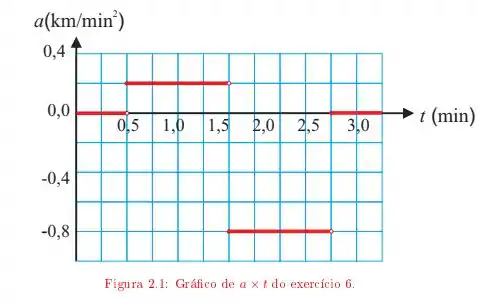
Determine o comprimento da rua.
Passo 1
E aí galera, tudo beleza?
Nessa questão, temos um carro que possui velocidade inicial, em , de e com uma aceleração que varia conforme o gráfico dado no enunciado. Também foi falado que quando o carro chega ao final da rua, ele para e passa a andar de ré.
Sabendo disso, precisamos determinar o comprimento da rua.
Alguma ideia?
Então, como é falado que o carro para ao chegar no final da rua, podemos usar as informações que recebemos pra calcular a distância que o automóvel percorreu até sua velocidade se tornar nula.
Podemos inclusive usar o gráfico da velocidade em função do tempo:
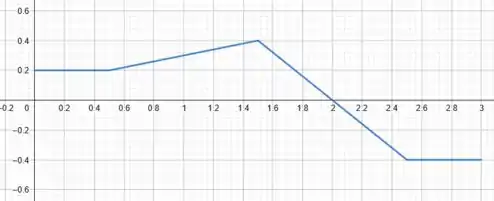
Assim, vemos claramente que a velocidade se torna nula em .
Vem com a gente que vai ficar tudo cristalino 😊
Passo 2
Queremos calcular a distância percorrida pelo carro até . Para isso, podemos calcular a área abaixo da curva azul.
Pra facilitar a geometria do nosso cálculo, vamos dividir essa região em partes:
Vamos então calcular a área abaixo da curva em cada uma dessas regiões.
Começando pela fase , temos uma velocidade constante de em .
Logo, a região abaixo da curva é um retângulo e temos:
Vamos agora para a fase . Temos que a velocidade vale:
(resultado que encontramos no item anterior).
Logo, a região abaixo da curva é um trapézio, com base menor:
E, base maior:
Com altura correspondente ao intervalo de tempo dessa fase, ou seja:
Logo, a área dessa região vale:
vamos agora para a região correspondente à fase ).
A altura desse triângulo é a velocidade inicial da fase e a base é metade do intervalo de tempo.
Analisando o gráfico vemos que essa velocidade vale:
Portanto:
Excelente!
Passo 3
Portanto, o comprimento da tua vai ser dado por:
Logo:
Prontinho gente!
Muito obrigado e até a próxima 😉