Um carro sobe uma ladeira com uma velocidade constante de e desce a ladeira com uma velocidade constante de . Calcule a velocidade escalar média da viagem de ida e volta.
Passo 1
Esse é um problema onde o trajeto é dividido em dois e pede-se a velocidade escalar média do trajeto. Vamos considerar todas as velocidades positivas, pois não levaremos em consideração as direções ( subindo ou descendo a ladeira) .
A primeira situação é subindo a ladeira, temos o seguinte esquema:
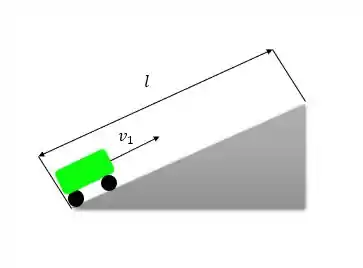
Na subida o carro vai percorrer a distância da ladeira com velocidade
O outro caso é a descida:
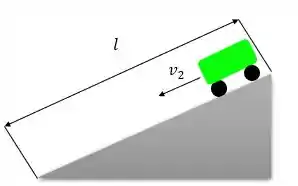
Na descida o carro de novo vai percorrer a distância e com velocidade .
Como o carro sobe e desce a ladeira, percorre a distância total , sendo assim a equação da velocidade escalar média para todo o percurso fica:
Onde é o tempo total dos dois movimentos, ou seja, é a soma do tempo para subir a ladeira com o tempo para descer a ladeira .
Precisamos então calcular o tempo pra cada um desses movimentos, bora lá?
Passo 2
Pra encontrarmos o tempo de subida vamos aplicar a equação da velocidade média somente pro movimento de subida, onde a velocidade é e a distância percorrida é
Substituindo:
Enfim temos o tempo de subida:
Passo 3
Fazendo o mesmo para o movimento de descida da ladeira, temos:
Substituindo :
Temos o tempo de descida.
Passo 4
O tempo total do movimento total será
Fazendo o MMC dos dois números temos:
Simplicando todo mundo por 20 temos:
Enfim simplicando a fração por 5:
Agora que temos o tempo total podemos calcular a velocidade escalar média de todo o percurso( Subida + Descida), assim usaremos a equação do ínicio com distância total .
Enfim temos: