Você dirige do Rio a São Paulo metade do tempo a e a outra metade a . Na volta, você viaja metade da distância a e a outra metade a . Qual é a velocidade escalar média do Rio a São Paulo, de São Paulo ao Rio e na viagem inteira? Qual é a velocidade média na viagem inteira? Plote o gráfico de em função de t para o item , supondo que o movimento ocorre no sentido positivo de . Mostre como a velocidade média pode ser determinada a partir do gráfico.
Passo 1
Esse exercício divide o caminho para ir do Rio a São Paulo em dois trechos. Nos dois trechos, você viaja por tempos iguais mas com velocidades diferentes.
Para calcular a velocidade escalar média, temos:
Agora precisamos calcular quanto que você andou no primeiro e no segundo trecho.
Passo 2
Para calcular a distância percorrida no primeiro trecho, faremos:
E no segundo trecho:
Passo 3
Agora, vamos substiruir os valores de e na equação da velocidade escalar média.
Passo 4
No trajeto de São Paulo ao Rio, você anda metade do trajeto com uma velocidade e a outra metade com outra velocidade. Diferente do item que você anda por tempos iguais com velocidades diferentes.
Vamos separa o trajeto em dois como fizemos no item anterior
A equação da velocidade escalar média vai ficar
Passo 5
Temos que descobrir o e o , faremos isso pela equação da velocidade
E o mesmo para o segundo trecho
Passo 6
Substituindo os valores de e na equação da velocidade escalar média
Fazendo m.m.c e cortando temos:
Passo 7
Para calcular a velocidade escalar média da viagem inteira, temos que o caminho para ir é igual ao de voltar logo
O tempo de ída e volta, vamos calcular usando as velocidades escalar média que acabamos de encontrar no item a de ída e no de volta
Assim aplicando a fórmula de velocidade escalar média temos
Fazendo m.m.c do denominador e cortando chegamos em:
Passo 8
a velocidade média da viagem inteira seria zero, pois o deslocamento seria zero
Passo 9
O gráfico de movimento do item será duas retas inclinas, onde a segunda está mais inclinada que a primeira, pois a velocidade no segundo trecho é maior que no primeiro. Fica algo assim:
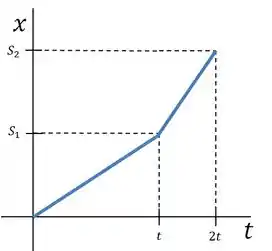
Tá meio fora de escala mas é só um esboço :)
Agora que temos o gráfico, basta traçar uma reta entre o ponto inicial e o ponto final , a tangente dessa reta é a velocidade média nesse trajeto.
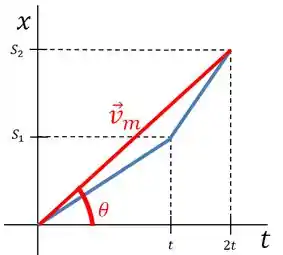
Resposta