Um motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
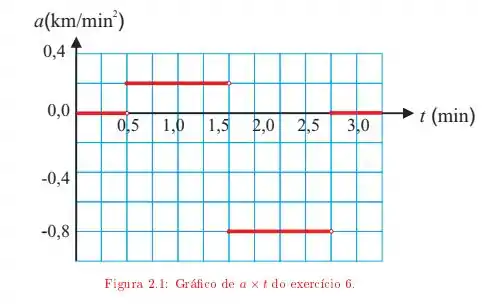
b) Determine a distância total percorrida pelo carro para este intervalo de tempo;
Passo 1
Olá gente, tudo certinho por aí?
Nessa questão, temos um carro que possui velocidade inicial, em , de e com uma aceleração que varia conforme o gráfico dado no enunciado. Basicamente, em , temos quatro fases diferentes:
Aceleração nula, logo velocidade constante:
Aceleração positiva e constante, logo a velocidade aumenta uniformemente:
Aceleração negativa e constante, logo a velocidade diminui uniformemente:
Aceleração nula, logo velocidade constante:
Precisaremos descobrir o valor dessa velocidade.
Juntando todas essas informações, no item anterior, conseguimos chegar no seguinte gráfico a velocidade em função do tempo:
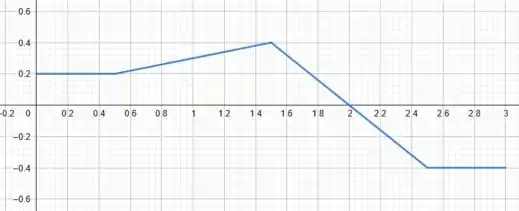
Assim, para calcular a Distância total percorrida pelo carro, basta calcularmos a área, em módulo, das regiões entre a nossa curva e o eixo .
Vamo nessa!
Passo 2
Vamos calcular a área abaixo da curva em cada uma das fases.
Começando pela fase , temos uma velocidade constante de em .
Logo, a região abaixo da curva é um retângulo e temos:
Vamos agora para a fase . Temos que a velocidade vale:
(resultado que encontramos no item anterior).
Logo, a região abaixo da curva é um trapézio, com base menor:
E, base maior:
Com altura correspondente ao intervalo de tempo dessa fase, ou seja:
Logo, a área dessa região vale:
Tudo tranquilo até aqui?
Passo 3
Bom, vamos agora para a região correspondente à fase ).
Temos dois triângulos simétricos, como queremos a área em módulo, não faz diferença que um esteja acima e o outro abaixo do eixo .
Portanto, vamos calcular a área de um deles e multiplicar por para obter .
A altura desse triângulo é a velocidade inicial da fase e a base é metade do intervalo de tempo.
Analisando o gráfico vemos que essa velocidade vale:
Portanto:
Por fim, na fase temos novamente um retângulo, pois a velocidade é constante.
Como a velocidade é de e o intervalo de tempo é de:
Ficamos com:
Para calcular a distância total percorrida , basta somarmos todos esses valores:
Portanto:
Terminamosss!!
Curtiram a solução? Responde Aí!