UFF, Sem Campus, Física 1, Listas de Física 1 - Profº Marcos Sergio - Lista 1, Questão 5c
5. Dois carros, e , se movem numa estrada retilínea. As equações horárias da posição dos carros e são respectivamente e , onde é medido em segundos e em metros.
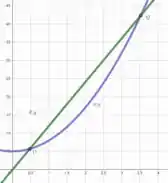
c) Faça um gráfico para os carros e .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Temos dois carros que viajam em uma rodovia retilínea onde as equações das posições são dadas para o carro como e para o carro como . Com isso queremos obter um gráfico da posição dos carros com relação ao tempo .
Lembra como fazemos isso? 😬
Anteriormente vimos que os carros se cruzam em e em , portanto os gráficos das posições devem se cruzar nesses pontos.
A função que descreve o carro é linear, portanto, o gráfico de é uma reta. Já é uma equação de segunda ordem, portanto seu gráfico será uma parábola.
Com essas informações somos capazes de esboçar os gráficos... 😬
Passo 2
Em o carro está em , já quando , o carro está em ... assim, uma única reta possui os pontos , e os pontos de intersecção entre e .
A função é uma parábola com vértice em , ou seja, .
Dessa forma, esboçando a reta e a parábola com vértice em e que cruza os pontos e interceptando a reta , temos
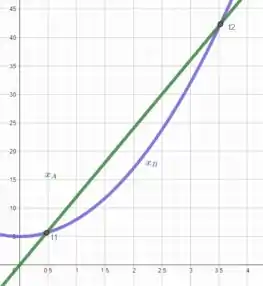
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
