Um determinado sistema triplo de estrelas consiste em duas estrelas, cada uma de massa , que giram na mesma órbita circular em torno de uma estrela central de massa . As duas estrelas situam-se nos extremos opostos de um diâmetro da órbita circular. Qual o período de revolução de cada estrela e sua energia mecânica?
Passo 1
Temos a seguinte situação:
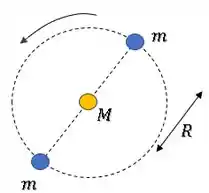
Vamos focar em apenas uma das estrelas em órbita, pois a situação é exatamente idêntica para a outra...
Quais são as forças atuando sobre cada uma das estrelas em órbita?
Existe uma força gravitacional entre as estrelas em órbita e além disso uma força gravitacional com a estrela central :
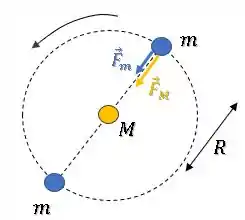
Como a órbita é circular, podemos dizer que a força resultante sobre a estrela atua como força centrípeta:
Assim, conseguimos uma relação com a velocidade orbital , e uma vez que temos a velocidade orbital, podemos encontrar o período e também sua energia mecânica.
Passo 2
Vamos calcular cada uma das forças gravitacionais.
A força gravitacional é dada por:
Como a distância entre a estrela central e a estrela em órbita é o proprio raio da órbita , a força gravitacional que ela exerce sobre a estrela em órbita é dada por:
Já a força entre as duas estrelas em órbita terá como a distância um valor igual a duas vezes o raio do órbita e além disso, ambas massas são iguai a :
Passo 3
Jogando na expressão da força centrípeta, temos:
Cortando o no denominador e a massa , temos:
Passando a raiz quadrada, conseguimos a velocidade orbital :
Passo 4
Para encontrar o período, podemos simplesmente usar a fórmula de velocidade média:
Se considerarmos o percurso de uma volta completa na órbita, temos que o deslocamento será o comprimento da circunferência da órbita:
Enquanto o tempo será o próprio período:
Então, temos que:
Isolando o período :
Passando aquele para dentro da raiz:
Tirando o da raiz:
Pronto, achamos o período do movimento.
Passo 5
Agora, vamos pensar na energia mecânica.
A energia mecânica será a soma da energia potencial com cada uma das outras duas estrelas com a energia cinética :
Lembrando que a energia potencial gravitacional é dada por:
Onde e são as massas dois corpos e é a distância entre eles.
Então, nossa energia fica assim:
Podemos ainda substituir o valor que já encontramos para a velocidade orbital :
Então:
Vamos abrir aquele último termo, para depois colocar os termos comuns em evidência:
Podemos colocar em evidência:
Somando as frações, temos: