Um objeto é abandonado do repouso a de altura da superfície da Terra. Despreze a resistência do ar.
Dados: ; (raio da Terra); (massa da Terra).
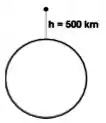
- Qual é a velocidade do objeto quando atinge o solo?
- Qual seria sua velocidade se a Terra fosse considerada plana?
- Qual é o erro percentual cometido supondo a Terra plana?
Passo 1
Já que o que se pede é velocidade, que tal trabalharmos com conservação de energia? A energia da bolinha antes é igual a soma das energias cinética e gravitacional no momento da chegada ao solo.
Passo 2
Substituindo valores,
Passo 3
Quando consideramos a Terra plana, a energia do corpo a uma altura passa a ser a energia potencial e não mais a energia gravitacional.
Para achar a velocidade no momento em que o objeto atinge o solo, continuaremos a usar a conservação de energia, com um diferencial:
Passo 4
Por fim, vamos calcular o erro percentual da velocidade. O que isso quer dizer? Quanto, em relação a velocidade do item a (a mais perto da realidade, visto que a Terra não é plana), foi a variação da velocidade do item b. Confuso, né? Matematicamente:
Queremos achar o valor de , assumindo como a velocidade no item a e como a velocidade no item b.
Passo 5
Então, vamos substituir os valores:
Resposta
- 3,6%