Um projétil é disparado verticalmente para cima, a partir da superfície da Terra, com uma velocidade inicial de 10 km/s. Desprezando a resistência do ar, calcule:
a) A distância h acima da superfície da Terra que o projétil alcança;
b) A velocidade de escape do projétil (aproximadamente);
c) Faça o gráfico da energia potencial gravitacional a partir da superfície da terra. Indique
claramente as escalas do gráfico mostrando aproximadamente o valor de h.
Dados aproximados:
massa da Terra ; raio da Terra ; constante de gravitação universal .
Passo 1
a) O projétil, inicialmente na superfície (altura igual ao raio da Terra: R) e velocidade 10 km/s, sofre atração gravitacional e sobe, diminuindo a velocidade, até chegar num ponto máximo (altura R+h), onde ele fica com velocidade nula.
Por isso, para resolver isso por conservação de energia, precisamos incluir o termo potencial gravitacional,
Onde é a massa do projétil e a massa da Terra.
Por conservação de energia,
Como no ponto máximo o projétil vai estar parado, sua energia cinética será zero. Na superfície, , o raio da Terra, e no ponto máximo será .
Botando do denominador em evidência, e cortando com o de cima:
Passo 2
b) A velocidade de escape é a velocidade mínima para o projétil sair da influência da fora gravitacional, ou seja, em que ele tenha energia cinética suficiente para compensar a energia potencial gravitacional,
Passo 3
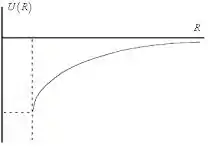
c) Vamos fazer o gráfico da energia potencial gravitacional, que é
Na superfície, a distância vai ser o próprio raio da Terra,
Para uma altura de 1000 km:
Para altura de
Para :
Para :
Para
E quando estiver muito longe da superfície (),
Resposta
a)
b)