Um objeto de massa é abandonado de uma altura acima da superfície de um planeta de massa e raio . Qual a rapidez do objeto ao chocar-se com a superfície do planeta?
Passo 1
O objeto é abandonado a uma altura da superfície do planeta:
Queremos saber a velocidade que ele atinge ao chegar na superfície desse planeta.
A força gravitacional aumenta conforme a distância diminui:
Como a força varia, a aceleração do corpo também varia, por isso fica um pouco mais difícil fazer essa questão simplesmente por cinemática, pois precisaríamos de uma integral...
Porém, existe um jeito bem tranquilo de resolver essa questão... por energia!

Por que esse é um bom caminho?
Isso porque a força gravitacional é uma força conservativa, ou seja, ela não retira energia do sistema.
Por isso, podemos dizer que a energia mecânica do sistema se conserva:
Assim, fica mais fácil de achar a velocidade final.
Passo 2
Inicialmente o corpo está em repouso, então ele não apresenta energia cinética, porém, apresenta uma energia potencial gravitacional:
A energia potencial gravitacional para um caso mais geral (quando não estamos apenas na superfície de uma planeta) é dada por:
Mas cuidado, a altura é a distância do corpo até a superfície e não a distância do corpo ao centro do planeta. Então, falta adicionar o raio do planeta :
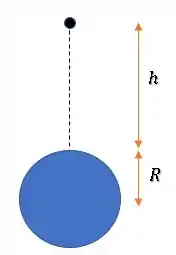
Assim, a energia mecânica inicial é:
Passo 3
Agora, vamos à situação final, quando o corpo atinge a superfície do planeta.
A energia mecânica final será a soma da energia potencial gravitacional com a energia cinética :
Mas qual é a distância agora?
A distância do corpo ao centro do planeta quando ele está na superfície é apenas o raio do planeta:
Então:
Passo 4
Voltando à conservação de energia mecânica, temos:
Podemos cortar a massa do objeto, isso mostra que a velocidade não depende da massa , ou seja, qualquer objeto que seja, chegaria com a mesma velocidade na superfície do planeta:
Isolando :
Vamos subtrair aquelas frações, fazendo um MMC:
Assim, achamos que: