Um sistema binário de estrelas consiste em duas estrelas idênticas, cada uma com massa , girando em torno do centro de massa do sistema. As estrelas estão em pontos opostos de uma mesma órbita circular de raio . Determine:
a) a intensidade da força gravitacional de uma estrela sobre a outra;
b) o módulo da velocidade orbital de cada estrela e o período da órbita;
c) a energia necessária para separar as duas estrelas até uma distância infinita.
Passo 1
O enunciado diz que as duas estrelas de massa estão em pontos opostos na mesma órbita:
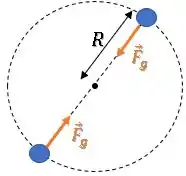
Passo 2
Na letra (a), queremos a força gravitacional entre eles.
A força gravitacional é dada por:
Onde e são as massas dos dois corpos, enquanto é a distância entre eles.
As massas dos dois corpos são e a distância entre eles é igual a duas vezes o raio da órbita :
Passo 3
Na letra (b), queremos o módulo da velocidade orbital de cada estrela e o período da órbita .
Como as estrelas realizam um movimento circular, podemos igualar a força gravitacional à expressão da força centrípeta :
A força centrípeta é dada por:
O raio da trajetória circular é , enquanto a massa é :
OBS: Estamos analisando apenas um dos corpos.
Assim, encontramos um valor para a velocidade orbital :
Podemos ainda colocar a constante para fora da raiz:
Passo 4
Ainda na (b), queremos o período .
Como já temos a velocidade orbital, podemos aplicar na expressão de velocidade média:
A jogada aqui é pensar em uma volta completa...
Quando a estrela completa uma volta, ela vai ter percorrido uma distância igual ao comprimento da circunferência da órbita:
Enquanto o tempo que demorou essa volta é a própria definição de período:
Então, juntando isso tudo na fórmula de velocidade média, temos:
Isolando o período , temos:
Para não ficar um dentro da raiz e outro fora dela, vamos passar o de fora para dentro da raiz. Então, ele entra na raiz elevado ao quadrado:
Passo 5
Na letra (c), queremos a energia necessária para separar as duas estrelas até o infinito.
Bom, enquanto essas estrelas realizam essa órbita, elas têm uma energia mecânica dada pela potencial gravitacional e cinética:
E essa energia mecânica tem um valor negativo, que vamos ver nas contas.
A energia necessária para separar elas até o infinito será o quanto de energia temos que acrescentar no sistema para que elas cheguem no infinito com energia zero.
Ou seja, energia cinética nula:
E energia potencial também nula, uma vez que a distância tende ao infinito:
Passo 6
Então, vamos calcular essa energia mecânica:
Mas essa velocidade orbital, nós já calculamos no item (b):
Então, temos:
Então, acresentando um valor de energia igual à essa energia mecânica , conseguimos separar as estrelas até uma distância infinita.
Resposta
(a)
(b)
(c)