Em uma esfera maciça e homogênea de massa M e raio 2R centrada na origem foram feitas duas cavidades esféricas de raio R. Os centros das cavidades esféricas estão nas posições e , como ilustrado na figura abaixo. Sabendo que uma massa m está na posição, faça o que é pedido abaixo.
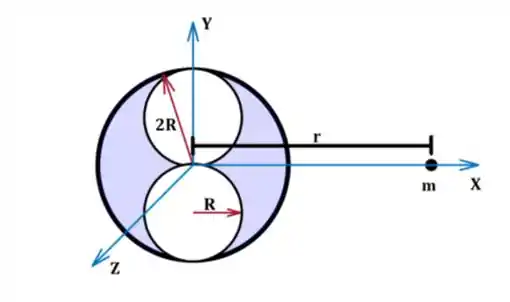
a) Calcule a força gravitacional que atua na partícula de massa m.
b) Admita que a partícula de massa m está em uma órbita circular de raio r > R no plano XZ. Calcule o período de rotação.
c) Calcule a energia potencial gravitacional do sistema ilustrado na figura ao lado.
Passo 1
a) A gente pode calcular a densidade da esfera de raio 2R assim:
Essa esfera de raio 2R, se fosse maciça, exerceria sobre a partícula uma força:
Eu coloquei esse pra indicar que essa força é um vetor que aponta no sentido positivo do eixo x.
Masssssss como foram tiradas duas esferas menores da esfera grande, temos que descontar isso.
Vamos calcular a massa das esferas retiradas:
A massa da esfera maior é:
Ou seja:
O módulo da força de atração entre as esferas retiradas e a partícula, é:
Para cada! Em que .
Passo 2
Esse negócio de vetores é um saco não é mesmo? Mas como a questão colocou ali, não tem como a gente resolver sem eles. Dá uma olhada aqui:
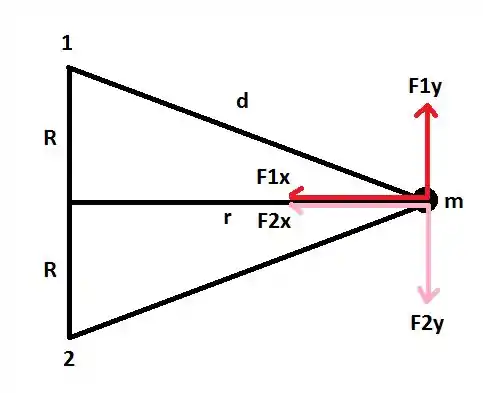
Os pontos 1 e 2 são os centros das esferas retiradas.
Escrevendo em vetores agora:
Então a força total (finalmente) vai ser:
Passo 3
b) Quando a massa estiver no plano XZ, a força vai ser igual à calculada no item anterior (graças a Deus). Essa força vai tá sempre apontando pra origem do sistema de coordenadas (ponto (0,0,0)) e vai ser a única força atuando na massa. Então vai ser igual à força centrípeta!
Podemos escrever:
Deus me free, é muita letra. Eu tirei o porque nessa conta só o que importa pra gente é o módulo da força.
Fazendo essa conta a gente vai achar:
Passo 4
c) Aqui a gente vai usar o princípio da superposição. A energia total vai ser a energia de interação da esfera de raio 2R com a massa m, menos a energia de interação entre as esferas menores e a massa m.
Então:
UFAAAAAA
Resposta
a)
b)
c)