Um satélite artificial encontra-se em uma órbita circular de raio em torno da Terra quando ativa seus motores e passa a uma órbita, também circular, de raio (). É correto afirmar que:
(a) A energia potencial associada à força gravitacional que a Terra exerce sobre o satélite aumenta na mudança de órbita.
(b) O trabalho realizado pela força gravitacional que a Terra exerce sobre o satélite é nulo na mudança de órbita.
(c) A energia cinética do satélite permanece inalterada na mudança de órbita.
(d) A energia mecânica do satélite permanece constante na mudança de órbita.
(e) A força gravitacinal que a Terra exerce sobre o satélite realiza trabalho positivo na mudança de órbita.
Passo 1
O enunciado diz que o satélite foi de uma órbita para uma órbita com raio maior :
Vamos fazer algumas considerações sobre os conceitos envolvidos nas opções.
Passo 2
(a) A energia potencial associada à força gravitacional que a Terra exerce sobre o satélite aumenta na mudança de órbita.
A energia potencial gravitacional é dada por:
Onde é a distância entre os corpos.
Como o raio da órbita aumentou de para , por esse valor estar no denominador, a energia ficará menor em módulo.
Entretanto, estamos tratando de valores negativos, então, diminuir em módulo na verdade é deixar o número cada vez mais próximo do zero, ou seja, aumentando essa energia potencial.
Quanto maior a distância, maior a energia potencial associada.
Assim, a afirmativa (a) está correta.
Passo 3
(b) O trabalho realizado pela força gravitacional que a Terra exerce sobre o satélite é nulo na mudança de órbita.
(e) A força gravitacinal que a Terra exerce sobre o satélite realiza trabalho positivo na mudança de órbita.
A força gravitacional sobre o satélite está sempre na direção radial à órbita:
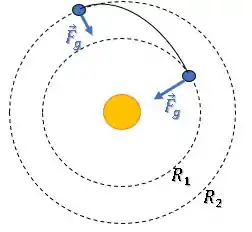
Uma força só gera trabalho se existir um deslocamento ou componente dele na sua direção.
Então, como houve um deslocamento radial na mudança de órbitas, houve um trabalho não nulo.
E esse trabalho foi positivo ou negativo?
Como o deslocamento radial foi no sentido contrário da força (aumentando o raio da órbita), então o trabalho foi negativo.
Ambas afirmativas são falsas.
Passo 4
(c) A energia cinética do satélite permanece inalterada na mudança de órbita.
Como o satélite está realizando uma órbita circular, sua velocidade orbital é dada por:
Ou seja, como houve uma mudança no raio da órbita, houve uma mudança na velocidade orbital também.
Passo 5
(d) A energia mecânica do satélite permanece constante na mudança de órbita.
Quando está numa órbita de raio a energia mecânica do satélite será
Podemos relacionar a velocidade com o raio da trajetória igualando a força gravitacional com a força centrípeta
Assim
Ou seja, ao aumentarmos o raio da trajetória a energia mecânica não é conservada! Então essa opção está errada.
E de onde vem a energia pra fazer essa mudança? Ela vem dos motores do nosso satélite ;)
Resposta
Letra (a)