A energia necessária para levar um satélite até acima da superfície da Terra é maior do que a necessária para colocá-lo em órbita, uma vez que ele já esteja naquela altura?
Dados:
Constante gravitacional:
Raio da Terra:
Massa da Terra:
Passo 1
Para responder isso, precisamos calcular duas energias, a primeira é a energia necessária para levar o satélite da superfície da Terra até uma altura de acima dessa superfície, enquanto a segunda é a energia necessária para colocá-lo em órbita nessa altura.
Depois de calculadas as duas energias vamos compará-las.
Passo 2
Para calcular a energia necessária para levar um satélite da superfície da Terra até uma altura de , basta calcularmos a diferença de energia potencial gravitacional .
A energia potencial gravitacional é dada por:
Vamos calcular a variação dessa energia:
Passo 3
Inicialmente, o satélite está na superfície da Terra, então sua distância ao centro do planeta é o próprio raio da Terra:
Assim:
Já na situação final, a distância do satélite ao centro da terra será sua altura da superfície somada ao raio da Terra:
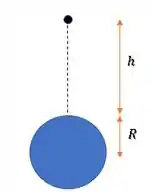
Passando para metros, temos:
Então:
Passo 4
Vamos calcular a variação:
Essa será a energia necessária no primeiro caso (levar o satélite a ).
Passo 5
Já no segundo caso (colocá-lo em órbita), o satélite já está naquela altura, então não haverá variação de energia potencial gravitacional.
Entretanto, para colocá-lo em órbita, precisamos fazer o satélite sair do respouso e atingir a velocidade orbital para aquela altura de da superfície.
Então, precisamos fornecer uma quantidade de energia igual a variação de energia cinética que o satélite em órbita vai ter a partir do repouso:
Passo 6
Para encontrar essa velocidade, basta igualarmos a força gravitacional com a força centrípeta:
A distância será a soma do raio da Terra com a altura a partir da superfície:
Já podemos deixar essa velocidade elevada ao quadrado na malandragem de substituir isso na energia cinética .
Passo 7
Assim, a variação de energia cinética será:
Passo 8
Agora, vamos comparar qual dos dois casos a energia é maior:
As duas energias e apresentam um termo multiplicando o fator , então vamos substituir os valores numéricos nesse termo e encontrar qual é maior
Para , temos:
Para , temos:
Agora já podemos comparar as duas energias:
Como ambas apresentam o fator em comum, podemos afirmar que a variação de energia cinética vai ser maior que a variação de energia potencial :
Assim, descobrimos que a energia para colocar o satélite em órbita é maior que a energia para levar o satélite da superfície da Terra até a altura de .
Então, a resposta da pergunta é não.
Resposta
Não, a energia para colocar o satélite em órbita é maior que a energia para levar o satélite da superfície da Terra até a altura de .