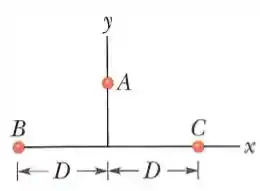
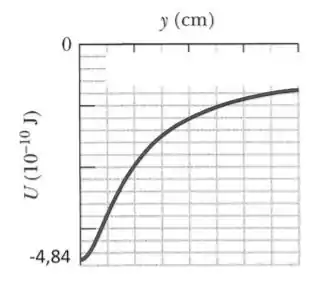
Uma partícula (partícula , de massa ) pode ser deslocada ao longo de um eixo desde uma distância infinita até a origem. A origem está localizada no ponto médio entre as partículas e , que têm massas iguais , e o eixo é perpendicular à linha que liga essas duas partículas. A distância é . O gráfico mostra a energia potencial do sistema de três partículas em função da posição da partícula no eixo , sendo que para a direita a curva tende assintoticamente ao valor de quando . Quais são os valores de e ?
.
Passo 1
Sabemos que a energia potencial gravitacional, no sistema mostrado, é dada por:
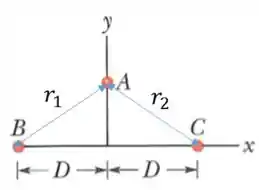
Mas, vendo a imagem, descobrimos que:
E, colocando em função de e :
Portanto, a expressão da energia é dada por:
Passo 2
Agora, com a expressão da energia do sistema, fica fácil!
Pelo gráfico, sabemos que, quando , a energia é , então:
Já para , temos que a energia é , então:
Sabendo que , podemos usar a segunda equação para encontrar o valor de :
Usando esse valor na primeira expressão: