Energia Gravitacional
O gráfico abaixo representa a aceleração da gravidade (em ) em função da distância ao centro de um asteróide esférico cujo raio é de
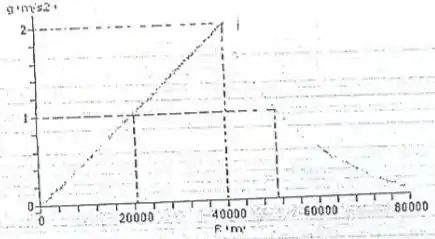
(a) Calcule a velocidade de escape de um corpo neste asteroide.
(b) Até que distância da superfície irá o corpo se ele deixar a superfície do asteroide com uma velocidade radial de ?
Passo 1
(a)
Do principio da Conservação de Energia:
Podemos deduzir a fórmula da velocidade de escape:
Mas, pela segunda Lei de Newton temos:
Onde é a aceleração da gravidade na superfície. Então:
Passo 2
(b)
Do princípio da Conservação de Energia:
Mas, sabemos que:
Substituindo isso:
Resposta
a)
b)
Exercícios de Livros Relacionados
Marte e a Terra têm um diâmetro médio de 6,9 × 10 3 k m e 1,3 × 10 4 k m , respectivamente. A massa de Marte é 0,11 vez a massa da Terra. (a) Qual é a razão entre a massa específica média de Marte e a
Sabendo que a aceleração da gravidade na Lua é 0 , 166 vezes aquela na Terra, e que o raio da Lua é 0,273R T , determine a rapidez de escape de um projétil lançado na superfície da Lua.
A força exercida pela terra sobre uma particula de massa m a uma distancia r( rR T ) do centro da Terra tem por magnitude m g R T 2 / r 2 , onde g = G M T / R T 2 . (a) Calcule o trabalho que você dev
Um corpo é lançado diretamente para cima da superfície da Terra, com uma rapidez inicial de 4,0k m / s . Qual é a altura máxima que ele alcança?
O escritor de ficção cientifica Robert Heinlein disse uma vez: “Se você pode ser colocado em órbita, então você está a meio caminho de qualquer lugar”. Justifique esta afirmativa comparando a energia