[Questão 12]
A figura ao lado mostra um foguete de massa que descreve uma órbita elíptica em torno da Terra, onde é a distância da Terra em relação ao centro da elipse e é o semi-eixo maior da elipse. A massa da Terra é . A única força que atua sobre o foguete é a atração gravitacional do planeta. No ponto A, o foguete tem velocidade de módulo . Com base nessas informações, responda as questões 11, 12 e 13.
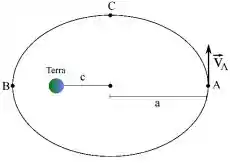
No ponto A da órbita, o foguete ilustrado na figura anterior aciona seus propulsores por alguns segundos, gerando uma força que o coloca em uma órbita circular de raio . Considerando que a força gerada pelos propulsores é instantânea e, portanto, que a distância do foguete ao planeta não muda durante sua aplicação, determine a variação de energia mecânica gerada pelos propulsores.
(A)
(B)
(C)
(D)
(E)
Passo 1
Quando o foguete aciona seus propulsores, sua velocidade muda de certa forma que sua órbita passa a ser circular.
Queremos achar a variação de energia mecânica ao longo dessa propulsão.
Passo 2
Como o enunciado despreza a mudança de posição do foguete nesse intervalo de tempo, suas energias potenciais gravitacionais serão as mesmas:
Então, temos:
Então, a variação de energia mecânica será apenas a variação de energia cinética .
Passo 3
Quem é a energia cinética inicial ?
Como o foguete tem velocidade inicialmente, sua energia cinética será:
Enquanto sua energia cinética final será:
Passo 4
Para encontrar a velocidade após a propulsão, vamos usar a informação de que sua órbita passa a ser circular.
Como a órbita é circular, a força gravitacional sobre o foguete age como força centrípeta, logo:
Já vamos deixar a velocidade elevada ao quadrado para entrar com esse valor na expressão de energia cinética.
Passo 5
Substituindo isso tudo na expressão de energia mecânica, temos:
Assim temos nossa resposta da letra (C):
Resposta
Letra (C)