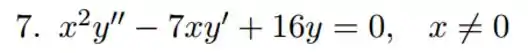
Passo 1
Uma equação de Euler de 2ª ordem aparece no formato
Olhando para a nossa EDO, vemos que é uma Equação de Euler de coeficientes
Se procurarmos soluções do tipo , temos a seguinte equação característica:
No nosso caso
Resolvendo encontraremos
Passo 2
Como , a solução da EDO é
Então ficamos com
Atenção! A solução geral não seria com esse módulo no logaritmo, mas como o enunciado nos diz que , isso permitiria que fosse negativo, então temos que adicioná-lo.
Resposta
Exercícios de Livros Relacionados
Nos problemas 35-40, resolva a equação diferencial dada fazendo a substituição x = e t . x 2 y ' ' - 3 x y ' + 13 y = 4 + 3 x
Nos problemas 29-34, usando variação dos parâmetros. x 2 y ' ' - x y ' + y = 2 x
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 8 x y ' + 6 y = 0
Nos problemas 1-22, resolva a equação diferencial dada. 4 x 2 y ' ' + y = 0
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 5 x y ' + 3 y = 0