Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Euler-Cauchy

Ver Teoria
Exercício 41235678910111213141516171819202122232425262728293031323334353637

Enunciado

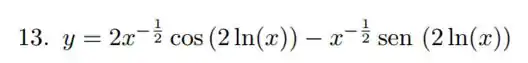
Passo 1

Essa é uma EDO tipo Cauchy-Euler.

4 x 2 y ' ' + 8 x y ' + 17 y = 0  

Para usar aquele nosso macete precisamos coloca-la na forma

x 2 y ' ' + α x y ' + β = 0

Para isso vamos dividir a equação inteira por 4 e ficar com

x 2 y ' ' + 2 x y ' + 17 4 y = 0

Agoooora podemos usar o macete! Nossa equação característica vai ser:

r 2 + α - 1 r + β = 0

Passo 2

Então vamos lá

α = 2

β = 17 4

Então a equação fica

r 2 + r + 17 4 = 0

Para encontrar as raízes

Δ = 1 - 17 = - 16

r = - 1 2 ± 2 i

Passo 3

Determinadas as raízes, vamos substitui-las na solução geral para casos onde Δ < 0

y x = x λ C 1 cos ⁡ ( μ ln ⁡ x ) + x λ C 2 sen ⁡ ( μ ln ⁡ x )

Como

λ = - 1 2   e   μ = 2

Então ficamos com

y x = x - 1 / 2 C 1 cos ⁡ ( 2 ln ⁡ x ) + x - 1 / 2 C 2 sen ⁡ ( 2 ln ⁡ x )

Passo 4

Por fim, precisamos utilizar as condições iniciais para resolver o PVI. Sabemos que

y 1 = 2   e   y ' 1 = - 3

Substituindo na equação

y x = x - 1 / 2 C 1 cos ⁡ ( 2 ln ⁡ x ) + x - 1 / 2 C 2 sen ⁡ ( 2 ln ⁡ x )

y 1 = 1 - 1 / 2 C 1 cos ⁡ ( 2 ln ⁡ 1 ) + 1 - 1 / 2 C 2 sen ⁡ ( 2 ln ⁡ 1 ) = 2

y x = C 1 cos ⁡ ( 0 ) + C 2 sen ⁡ ( 0 ) = 2

C 1 = 2

Precisamos derivar nossa solução para utilizar a segunda condição

y ' x = - C 1 2 x 1 2 cos ⁡ 2 ln ⁡ x + C 1 x - 1 2 - sen ⁡ 2 ln ⁡ x 2 x - C 2 2 x 1 2 sen ⁡ 2 ln ⁡ x + C 2 x - 1 2 cos ⁡ 2 ln ⁡ x 2 x

Aplicando y ' 1 = - 3

y ' x = - C 1 2 cos ⁡ 0 - 2 C 1 sen ⁡ 0 - C 2 2 sen ⁡ 0   + 2 C 2 cos ⁡ 0 = - 3

- C 1 2 + 2 C 2 = - 3

C 2 = - 1

Então nossa solução fica

y x = 2 x - 1 / 2 C 1 cos ⁡ ( 2 ln ⁡ x ) - x - 1 / 2 C 2 sen ⁡ ( 2 ln ⁡ x )

Prontinho! Resolvido nosso PVI!

Resposta

Exercícios de Livros Relacionados

Nos problemas 35-40, resolva a equação diferencial dada fazendo a substituição x = e t . x 2 y ' ' - 3 x y ' + 13 y = 4 + 3 x
Nos problemas 29-34, usando variação dos parâmetros. x 2 y ' ' - x y ' + y = 2 x
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 8 x y ' + 6 y = 0
Nos problemas 1-22, resolva a equação diferencial dada. 4 x 2 y ' ' + y = 0
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 5 x y ' + 3 y = 0