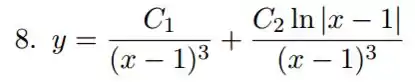Passo 1
Essa é uma EDO tipo Cauchy-Euler. Não vamos nos estressar inicialmente como esse que aparece nos dois primeiros termos. Vamos resolve-la como se fosse
E resolver isso é moleza demais! Já sabemos aquele macete que diz que nossa equação característica vai ser
Quando tivermos esse formato.
Passo 2
Então vamos lá
Então a equação fica
Que é facílimo de encontrar as raízes
Passo 3
Determinadas as raízes, vamos substitui-las na solução geral para casos onde
Então ficamos com
Passo 4
Maaaas, não vamos esquecer que lá no início, ignoramos aquele . Agora temos que substituir onde temos por .
Nossa solução vai ser
Essa é nossa solução!
Resposta
Exercícios de Livros Relacionados
Nos problemas 35-40, resolva a equação diferencial dada fazendo a substituição x = e t . x 2 y ' ' - 3 x y ' + 13 y = 4 + 3 x
Nos problemas 29-34, usando variação dos parâmetros. x 2 y ' ' - x y ' + y = 2 x
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 8 x y ' + 6 y = 0
Nos problemas 1-22, resolva a equação diferencial dada. 4 x 2 y ' ' + y = 0
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 5 x y ' + 3 y = 0