Encontre todos os valores de para os quais todas as soluções de
tendem a zero quando tende a infinito.
Passo 1
Olhando para a EDO, vemos que é uma Equação de Euler de coeficiente ( é o que queremos encontrar).
Se procurarmos soluções do tipo , temos então a seguinte equação característica:
Como nós não conhecemos , não sabemos se , ou , então, vamos ter que analisar a questão para cada um desses três casos.
Passo 2
Supondo que
- Encontrar o intervalo de .
- Encontrar a solução geral de
- Encontrar que faz
- Fazer a interseção entre os itens 1 e 3
Lembra como resolve esse tipo de inequação? Vamos fazer um esboço da parábola para você entender melhor:
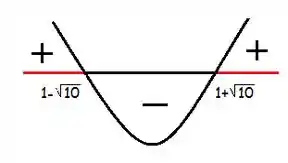
Queremos a parte positiva (acima do eixo horizontal). Pela figura, vemos que isso ocorre em:
Certo, então estamos analisando apenas esses valores de , que fazem o ser positivo.
Nesse caso, temos duas raízes reais distintas:
E as soluções da EDO são do tipo
O problema pede que as soluções tendam a zero quando , não é? Em outras palavras, queremos:
Isso ocorre quando for elevado a um número negativo, ou seja, quando e .
Portanto, precisamos de raízes negativas:
Somando as inequações, encontramos
Cuidado! Lembre-se de que estamos analisando apenas uma parte dos ’s: e . Queremos dentro desses valores, portanto a interseção de com esses valores. Isso nos dá
Passo 3
Supondo que
- Encontrar o intervalo de
- Encontrar a solução geral de
- Encontrar que faz
- Fazer a interseção entre os itens 1 e 3
Então, agora estamos analisando apenas esses valores de , que fazem ser igual a zero.
Nesse caso, encontramos a raiz dupla da equação característica:
As soluções da Equação de Euler são do tipo:
O problema pede que as soluções tendam a zero quando , ou seja:
Novamente, isso ocorre quando for elevado a um número netagivo, ou seja, quando , pelo mesmo motivo que vimos no caso anterior.
Queremos, então:
A interseção de com e é
Passo 4
Supondo que
- Encontrar o intervalo de
- Encontrar a solução geral de
- Encontrar que faz
- Fazer a interseção entre os itens 1 e 3
É exatamente o oposto do que vimos no primeiro caso, a mesma parábola, mas agora queremos a parte do meio, veja:
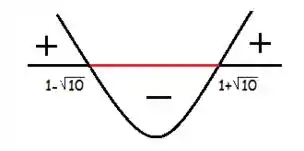
Logo, estamos analisando os seguintes valores de : .
Nessa região temos negativo, o que nos leva a duas raízes complexas para a equação característica:
Veja que, para colocar em evidência, tivemos que mudar o sinal do que está dentro da raiz!
As soluções da Equação de Euler são do tipo:
O problema pede que as soluções tendam a zero quando , ou seja:
Esse limite depende que seja elevado a um número negativo. Caso contrário, e o limite da solução também não será zero. Logo, queremos
A interseção disso com os valores de que estamos analisando é:
Passo 5
Calma, já está terminando! Temos então três soluções para os três casos possíveis de . Logo, todos os valores que encontramos no final de cada um dos casos atendem ao pedido do problema. Vamos, então, unir essas respostas!
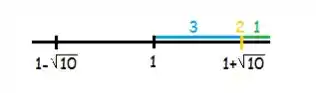
Juntando isso tudo, temos nossa resposta final: .