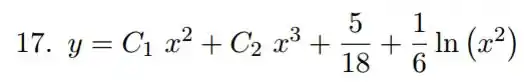Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Euler-Cauchy

Ver Teoria
Exercício 13123456789101112141516171819202122232425262728293031323334353637

Enunciado

Passo 1

Vamos resolver a EDO

x 2 y ' ' - 4 x y ' + 6 y = ln ⁡ x 2

Usando a substituição

x = e t

Para isso, vamos chamar

y x = g

Logo

g ' = y ' e t

g ' ' = y ' ' e 2 t + y ' e t

Rearranjando temos

y ' ' e 2 t = g ' ' - g '

E aplicando na EDO

g ' ' - g ' - 4 g ' + 6 g = 2 t

g ' ' - 5 g ' + 6 g = 2 t

Passo 2

Vamos primeiro resolver essa nova equação como se fosse homogênea

g ' ' - 5 g ' + 6 g = 0

Encontrando a equação característica

r 2 - 5 r + 6 = 0

E as raízes são

r = 3   e   r = 2

Daí, a solução homogênea que encontramos é

g h = C 1 t 2 + C 2 t 3

Passo 3

Agora vamos resolver a parte não homogênea. Supondo uma solução particular

g p = A t + B

g ' = A

g ' ' = 0

Substituindo na EDO temos

- 5 A + 6 A t + 6 B = 2 t

Assim, encontramos

A = 2 6   e   B = 5 18

Ou seja, a solução particular é

g p = 2 t 6 + 5 18

Passo 4

A solução geral é

g = g h + g p

g = C 1 t 2 + C 2 t 3 + 2 t 6 + 5 18

Maaaaas nossa variável não é t , então voltando para x .

y x = C 1 x 2 + C 2 x 3 + ln ⁡ x 2 6 + 5 18

Resposta

Exercícios de Livros Relacionados

Nos problemas 35-40, resolva a equação diferencial dada fazendo a substituição x = e t . x 2 y ' ' - 3 x y ' + 13 y = 4 + 3 x
Nos problemas 29-34, usando variação dos parâmetros. x 2 y ' ' - x y ' + y = 2 x
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 8 x y ' + 6 y = 0
Nos problemas 1-22, resolva a equação diferencial dada. 4 x 2 y ' ' + y = 0
Nos problemas 1-22, resolva a equação diferencial dada. x 2 y ' ' + 5 x y ' + 3 y = 0