Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Centrípeta

Ver Teoria
Exercício 412356789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

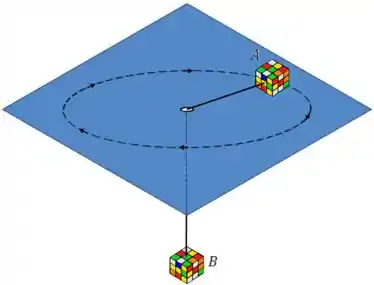
Um aluno, meio nerd, decide fazer uma experiência em uma mesa de ar. Ele solta um cubo de Rubik nessa mesa, preso por um fio que passar por um furo no centro da mesa, e na outra ponta do fio está outro cubo de Rubik, como mostrado na figura. Esse cubo sobre a mesa está realizando um movimento circular, de velocidade angular ω . Determine o raio do movimento considerando que o cubo pendurado está em repouso, e a massa de ambos os cubos é m .

Passo 1

Normalmente começamos um problema com vários blocos, fazemos o DCL do sistema. Neste caso, como temos o cubo B em repouso e o cubo A se movimentando circularmente, fazer o sistema pode ser algo mais complicado, então iremos montar as equações para cada bloco.

Os dados do problema são

Dados m ω

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

Para o bloco B

Vamos responder as perguntas do passo a passo para colocar as forças

  1. A massa dele é considerada?

    2. Sim, ele tem massa.

  2. Ela esta encostada em alguma superfície?

    3. Não, o bloco não está apoiado em nenhuma superfície.

  3. Tem algum fio?

    4. Sim, existe um fio.

  4. Tem mola?

    5. Não, não existe mola atuando.

  5. Tem atrito?

Não, não existe atrito.

Seu DCL fica

Passo 2

Como o sistema está em repouso temos equilibro em ambos os eixos. Vamos fazer o equilíbrio no e i x o   y , que é o eixo onde as forças atuam.

P b = T

T = m g

Passo 3

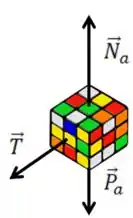
Para o bloco A

Vamos responder as perguntas do passo a passo para colocar as forças

  1. A massa dele é considerada?

    2. Sim, ele tem massa.

  2. Ela esta encostada em alguma superfície?

    3. Sim, o bloco está apoiado na mesa.

  3. Tem algum fio?

    4. Sim, existe um fio.

  4. Tem mola?

    5. Não, não existe mola atuando.

  5. Tem atrito?

Não, não existe atrito, pois o bloco está sobre uma mesa de ar.

Seu DCL fica

Passo 4

Como esse cubo faz um movimento circular, sabemos que a força resultante na direção do centro da curva é a força centrípeta. A única força que está nessa direção é a tração

F c p = T

m v 2 R = m g

Para resolver essa equação precisamos da velocidade.

Passo 5

Lembrando do capitulo de movimento circular podemos relacionar a velocidade com a velocidade angular da seguinte forma

v = ω R

Lembrando que, nesse caso, ω < 0 , pois, pelo desenho, o cubo está se movendo no sentido horário. Isso não vai alterar o resultado final, mas fica aí o bizu!

Passo 6

Substituindo na equação da força centrípeta

m ω R 2 R = m g

ω 2 R = g

R = g ω 2

Resposta

R = g ω 2

Exercícios de Livros Relacionados

Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a 29k m / h faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é 0,32 ?
Em um brinquedo de parque de diversão, um carro se move em uma circunferência vertical na extremidade de urna haste rígida de massa desprezível. O peso do carro com os passageiros é 5,0k N e o raio da
Um estudante que pesa 667N está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal F N exercida pelo assento sobre o estudante é 556N . (a) O
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =107m , que a massa
Um bonde antigo dobra urna esquina fazendo uma curva plana com 9,1m de raio a 16k m / h . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?